INTRODUCTION

Le champ magnétique terrestre est connu des hommes depuis fort longtemps. Les plus anciens textes retrouvés qui font référence à la boussole sont chinois et remontent au premier siècle de notre ère. Mais l'explication du phénomène restera longtemps mystérieuse, puisque l'on pense encore au XIII^e siècle que la boussole pourrait pointer vers l'étoile polaire. L'idée que l'orientation de la boussole est liée à la Terre elle même, est mentionnée pour la première fois par le Dr. William Gilbert (médecin de la reine Elisabeth I d'Angleterre). En 1600, il compare dans son De Magnete la Terre à un ``énorme aimant'' proposant ainsi le premier modèle de génération du champ magnétique terrestre (c.f. figure 0.1.)

La démonstration que l'essentiel du champ magnétique est bien d'origine interne vient bien plus tard, elle est faite par Carl Friedrich Gauss en 1839. Gauss invente les ``Harmoniques Sphériques'' pour décrire le champ (nous utiliserons ces mêmes harmoniques dans cette thèse), et déduit de son potentiel l'origine interne du champ. La question de son origine reste cependant encore entière. Revenons au XVII^e siècle, Henry Gellibrand, professeur d'Astronomie au Gresham College à Londres, publie en 1634 une découverte étonnante. Reprenant les mesures du champ faites par ses deux prédécesseurs William Borough (1580) et Edmund Gunter (1622) en lesquels il avait grande confiance, il constate une variation dans le temps du champ au même lieu, de plus de 7^o.

Cette variation lente du champ (par opposition aux variations rapides et quasi périodiques d'origine externe), s'appellera plus tard ``variation séculaire''. Cette observation surprenante paraît difficilement conciliable avec l'hypothèse d'un aimant permanent bien ancré à l'intérieur de la planète... Descartes reprend pourtant, en 1644, dans les Principia (Part IV, § 133 à 183) l'aimantation permanente proposée par Gilbert, et tente d'expliquer l'évolution temporelle du champ en un même lieu par l'activité des hommes qui ``tirent continuellement du fer de certains endroits de la Terre, et le transportent en d'autres'', conjugué au fait qu' ``il y a eu autrefois des mines de fer en des lieux où il n'y en a plus, pource qu'elles s'y font corrompuës avec le temps''. Il propose également une interprétation assez singulière du magnétisme à base de ``parties canelées'' (qui sont les petites ``viroles'' de la figure 0.2, et qui marquent ce que l'on appellerait sans doute les lignes de force du champ) et de ``pores'' dont certains corps sont pourvus, comme l'intérieur de la Terre, et les aimants (qui sont les petits cercles périphériques sur la figure 0.2).

Au début du XIX^e siècle, André-Marie Ampère propose un modèle différent pour expliquer le magnétisme terrestre, le champ magnétique de la Terre serait dû à des courants électriques qui y circulent :

Ampère envisage alors une pile chimique comme source des courants. En 1831, Michael Faraday s'intéresse également au problème de l'origine électrique possible du champ géomagnétique, et envisage des courants induits par la rotation de la Terre (repris dans Experimental researches in electricity). La même année, Peter Barlow vérifie expérimentalement que l'existence de courants électriques dans la Terre peut expliquer les observations. Le modèle de Barlow consiste en une sphère en bois, de ``16 pouces'' de diamètre (environs 40 cm), dans laquelle il grave des rainures à l'équateur et des parallèles tous les 4 degrés, ainsi qu'une rainure verticale d'un pôle à l'autre. Il enroule autour d'elle un fil de cuivre de 90 pieds (environ 27 mètres), en passant de parallèle en parallèle. Une fois parcouru par un courant, son modèle reproduit si bien l'orientation de la boussole (déclinaison et inclinaison) qu'il y dessine, pour plus de réalisme, des continents. Il conclut sur l'origine électrique probable du magnétisme terrestre :

Le problème de l'origine de ces courants reste cependant entier, Barlow envisage un effet thermo-électrique. Aucune réponse définitive n'est apportée à la question de l'origine des courants. Arago écrit ``Il faut donc se résigner, à l'époque actuelle, à réunir les mesures qui serviront de bases aux recherches de nos successeurs''. Qu'en est il donc des mesures du champ ? On sait depuis le XV^e siècle que la boussole n'indique pas tout à fait le nord, mais forme avec sa direction un angle appelé déclinaison magnétique. Robert Norman observe au XVI^e siècle que l'aiguille n'est pas non plus parfaitement horizontale [La première observation de l'inclinaison magnétique est en fait à attribuer à Georg Hartmann, qui la relate dans une lettre au Duc de Prusse, mais cette information étant restée cachée, Robert Norman la re-découvre indépendamment]. Lors de la fabrication de boussoles, il remarque que si ses aiguilles sont bien équilibrées avant d'être magnétisées, il doit alourdir le pôle sud pour équilibrer l'aiguille une fois celle-ci aimantée [Il travaillait à la latitude de Londres !]

Il démontre ensuite l'existence de l'inclinaison à l'aide d'une expérience consistant à maintenir une aiguille aimantée en suspension dans un liquide (voir figure 0.3).

La troisième composante du champ magnétique, l'intensité, est sans doute la plus difficile à mesurer. Les premières mesures sont faites, par analogie avec la mesure du champ de gravité (par observation des oscillations d'un pendule), en comptant les battements d'une boussole écartée de sa position d'équilibre.

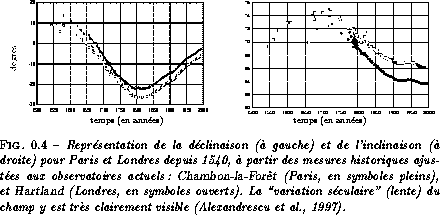
Pour mesurer de manière systématique ces composantes, Carl Friedrich Gauss a créé en 1839 à Göttingen le premier observatoire magnétique. En France, le premier observatoire est installé en 1883 au parc de Saint-Maur (transféré en 1901 près de Versailles, il est depuis 1936 à Chambon-la-forêt, voir Alexandresku et al. 1997). On apprend beaucoup sur le champ magnétique de la Terre par son observation. Outre des variations rapides et de faibles amplitudes (d'origine externe), on décrit la variation séculaire, cette évolution lente et assez régulière du champ (voir figure 0.4). Elle peut entraîner une variation de l'intensité du champ de quelques pour-mille par an. Ces variations ont de quoi impressionner. Arago commence le chapitre de ses oeuvres consacré au magnétisme terrestre par cet avertissement :

et James Clerk Maxwell note à la fin de son chapitre sur le magnétisme terrestre de son traité d'électricité et de magnétisme :

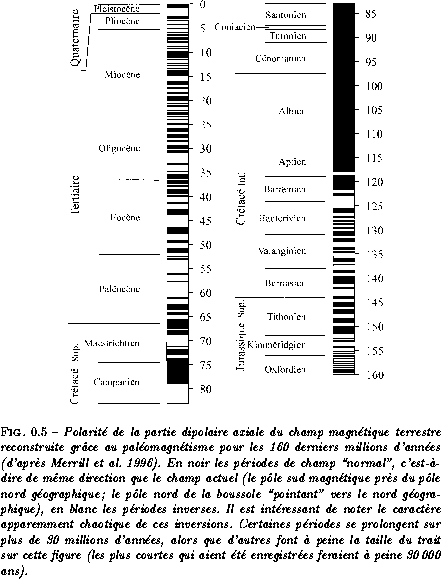
Malgré l'absence de moyens d'accès directs aux profondeurs de la Terre, des caractéristiques plus étonnantes encore du champ furent découvertes ensuite en étudiant les traces des temps anciens. A la fin du XIX^e siècle, on s'aperçoit que l'orientation de l'aimantation de certaines roches coïncide avec le champ terrestre, c'est l'aimantation rémanente naturelle, qui est à la base du paléomagnétisme et de l'archéomagnétisme. Des laves en se refroidissant ont enregistré le champ magnétique ambiant au moment de leur solidification. On peut donc envisager, en lisant convenablement ces enregistrements, d'étudier les variations du champ magnétique de la Terre sur des échelles de temps bien plus grandes que celles jusque là accessibles (par observations directes). Grâce aux études paléomagnétiques, la connaissance du champ magnétique terrestre s'accroît considérablement. On apprend que celui-ci existe depuis au moins 3,5 milliards d'années (les plus vieux enregistrements remonteraient même à 3,8 milliards d'années), et surtout, on explore ses variations sur de grandes échelles de temps. En 1906, Bernard Brunhes découvre que certains échantillons présentent une aimantation rémanente dont la direction est opposée à celle du champ actuel ! Le champ magnétique de la Terre se serait donc inversé au cours de son histoire. L'existence de ces inversions du champ fut controversée jusque vers 1950 (voir Valet et Courtillot, 1992). Elle est à présent bien établie (voir figure 0.5).

Aucun des mécanismes envisagés jusque là pour expliquer le champ géomagnétique ne peut rendre compte d'une telle variabilité dans le temps. En 1919, Sir Joseph Larmor propose trois possibilités pour expliquer le champ magnétique du soleil. A la fin de son article, il note que seule l'une d'entre elles pourrait être appliquée à la Terre, mais reste prudent, car cela nécessiterait que des régions profondes de notre planète soient fluides. Il décrit cette possibilité en ces termes :

En simplifiant quelque peu, elle peut se résumer ainsi : si l'on admet qu'un champ magnétique existe, et s'il baigne dans un fluide conducteur en mouvement, ces mouvements d'un conducteur dans un champ magnétique peuvent induire des courants. A ces courants est associé un second champ magnétique, et si celui-ci vient renforcer le champ déjà existant, on peut alors obtenir une dynamo [Elle a ceci de commun avec la dynamo de vélo qu'elle transforme de l'énergie cinétique en énergie magnétique. Mais c'est tout ! La dynamo de vélo utilise pour cela un aimant, elle n'est pas ``auto-excitée''. De plus les courants y sont contraints à l'aide de bobinages, alors que le noyau dans son ensemble est un conducteur. ] Peu de temps après, le sismologue Beno Gutenberg montre, par l'observation des temps d'arrivée d'ondes sismiques ayant traversé la planète, que la Terre possède un noyau. Retardé par la seconde guerre mondiale, Walter Elsasser s'appuyant sur la découverte de Gutenberg, publie en 1946 un travail divisé en trois articles, reprenant et formalisant le mécanisme proposé par Larmor, jetant les bases d'une théorie dynamo dans le noyau fluide de la Terre. Cette théorie est la seule proposée qui permette de rendre compte, tant de la variation rapide des termes non dipôles du champ magnétique (variation séculaire), que des inversions de sa partie dipôle. Elsasser sera suivi par Bullard en 1949, et bien d'autres après. Il serait certainement passionnant de pouvoir décrire l'histoire de la théorie dynamo, et de connaître les contributions des chercheurs qui l'ont développée, malheureusement cela sort du cadre de cette introduction [Façon à peine voilée de dire que j'en suis malheureusement encore incapable ! ] Je me borne à rappeler deux événements d'importance. En 1934, Thomas Cowling démontre qu'un champ purement axisymétrique ne peut être entretenu par une action dynamo. C'est le premier théorème anti-dynamo (d'autres sont découverts par la suite). Il est de taille, car le champ de la Terre étant essentiellement dipolaire axial, il était tentant d'imaginer un modèle purement axisymétrique. On peut alors se demander s'il n'existe pas un théorème anti-dynamo général ! En 1958, Herzenberg et Backus exhibent indépendamment des familles de mouvements capables de faire croître un champ magnétique, un tel théorème ne saurait donc exister. Depuis lors, la théorie dynamo étant la seule à pouvoir rendre compte des observations est très largement acceptée, elle n'a cependant jamais été démontrée. Ce que l'on sait aujourd'hui sur l'intérieur de notre planète nous donne-t-il de nouvelles pistes ? Les progrès de la sismologie ont été rapides et considérables. En 1981, Dziewonski et Anderson proposent un modèle de Terre en couches sphériques concentriques, que l'on appelle PREM (Preliminary Reference Earth Model), et qui sert aujourd'hui encore de référence. Ce modèle est établi à partir des observations sismologiques (ondes et modes normaux), ainsi que de la masse et du moment d'inertie terrestres. Il apporte une grande quantité d'informations sur le noyau terrestre. Il spécifie la densité, , en fonction de la distance au centre de la Terre (premier graphe de la figure 0.6. On peut vérifier qu'elle varie assez peu dans le noyau, avec une légère discontinuité entre la graine et le noyau liquide.

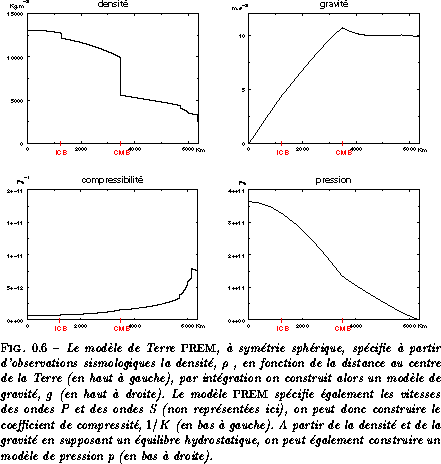
On peut en déduire, par intégration, un modèle de gravité. On montre que, pour une Terre à symétrie sphérique et homogène, la pesanteur varierait linéairement avec la distance au centre. Cela dérive de la formule de Gauss sur une sphère de rayon r, [On note que seules les masses internes à la sphère considérée ont en définitive un effet (l'intégrale sur la sphère s'annulant pour les masses externes). ]

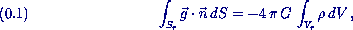
où G est la constante de gravitation universelle, et n la normale sortante à la sphère, d'où avec nos hypothèses

On vérifie alors que, bien que l'hypothèse d'homogénéité soit fausse, le profil de gravité ne diffère que très peu d'un profil linéaire dans le noyau (deuxième graphe de la figure 0.6). Le modèle PREM spécifie également les vitesses des ondes P et des ondes S (non représentées ici), on peut donc construire le coefficient de compressibilité, 1/K, (troisième graphe de la figure 0.6). On note que le noyau est très faiblement compressible (de l'ordre de 10^-12 Pa^-1). On peut également estimer un profil de pression en supposant un équilibre hydrostatique dans le noyau, on a alors

ce qui donne un modèle de pression hydrostatique dans la Terre (quatrième graphe de la figure 0.6). On le voit, l'approche sismologique fournit des informations très riches sur l'intérieur de la Terre. D'autres informations importantes sont apportées par différentes branches des sciences. La géochimie aide à comprendre la composition du noyau. A partir des résultats de l'observation des météorites, on pense que le noyau terrestre est essentiellement constitué de fer mélangé à des éléments plus légers (sans doute un mélange de divers éléments: soufre, oxygène, silicium,...). Ceci est confirmé par l'observation du moment d'inertie de la planète. Les caractéristiques du fer (viscosité, conductivité électrique, conductivité thermique) aux conditions de température et de pression du noyau sont très mal connues. On les estime par extrapolation de mesures faites à des conditions moins extrêmes (mais déja très difficiles à atteindre). La connaissance de la conductivité du noyau liquide est très importante, car elle permet d'estimer en combien de temps les courants y circulant seraient dissipés par effet Joule s'ils n'étaient pas entretenus. C'est le temps diffusif, ou constante de temps de Cowling, qui correspond au temps caractéristique de diffusion du champ dans un conducteur au repos. Si est le coefficient de diffusion magnétique construit sur la conductivité et r le rayon du noyau, cette constante est de l'ordre de r²/ (soit environ 100000 ans pour la Terre). On peut calculer plus précisément cette constante dans le cas d'une sphère: r²/(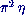) (dans une sphère, le dipôle diffuse avec cette constante de temps, c'est le mode le plus lentement décroissant), soit environ 10000 ans pour la Terre. Or, on l'a vu, le paléomagnétisme nous apprend que le champ magnétique de la Terre existe depuis au moins 3,5 milliards d'années. C'est un point important, car cela justifie que l'on cherche la source des courants qui sont à son origine. On a pu reconstruire les variations du champ sur des échelles de temps diverses. L'archéomagnétisme, grâce aux enregistrements du champ dans des fours de potiers ou dans des briques (datés indépendamment par ailleurs), a permis de reconstituer l'inclinaison et la déclinaison du champ sur la période historique. Les mesures fournissent une courbe qui se raccorde avec une précision étonnante avec celles décrite par les mesures effectuées dans les observatoires (voir figure 0.7) et permettent une observation plus étendue de la variation séculaire.

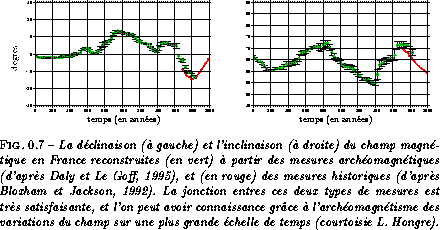
La mesure du champ en plusieurs points du globe permet d'en connaître l'allure spatiale. Si l'on admet que les sources du champ géomagnétique sont bien dans le noyau (c'est-à-dire à des profondeurs supérieures à 2891 km), et si le manteau n'est pas trop conducteur de l'électricité, on peut alors prolonger le potentiel de Gauss duquel dérive le champ et en déduire le champ sortant à la frontière Noyau-Manteau (voir figure 0.8).

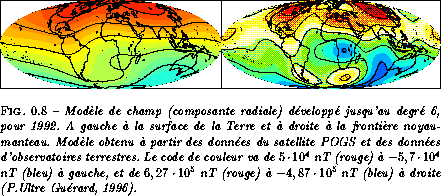
Il est important de noter que si la décroissance du potentiel de Gauss en fonction du degré de l'harmonique (en l(l+1)) suffirait à expliquer qu'à la surface de la Terre (donc ``loin des sources'') le champ soit dominé par le dipôle, ces prolongements montrent que le champ est déjà très largement dipolaire axial à la frontière avec le noyau. On peut également, en calculant la décomposition en harmoniques sphériques du champ, illustrer la variation séculaire du champ par sa représentation à diverses époques à l'interface noyau-manteau (figure 0.9).

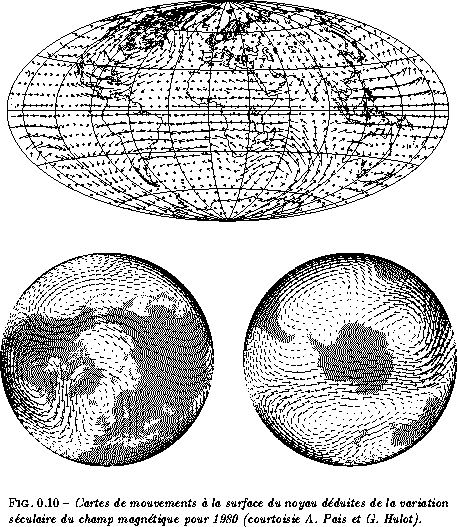
Enfin, aidé d'hypothèses assurant l'unicité, on peut déduire de ces variations du champ à la surface du noyau les mouvements tangentiels qui ont pu les causer. On établit alors des cartes de mouvements à la surface du noyau [Réalisées sous l'hypothèse de mouvement de grande échelle, et du ``flux gelé'' (diffusion négligeable devant le transport). ] (voir figure 0.10).

Notre connaissance du noyau de la Terre et du champ magnétique a donc extrêmement progressé, et pourtant, on ne sait toujours pas comment le champ induit par les mouvements du fer liquide renforce le champ principal, pourquoi le champ est de nature essentiellement dipolaire, pourquoi ce dipôle est en moyenne aligné avec l'axe de rotation de la Terre, ni pourquoi le champ varie et s'inverse... Ces dernières années ont vu l'apparition de nombreuses études numériques ayant pour but de faire progresser notre compréhension de ces questions: modèles presque axisymétriques, modèles hyper-visqueux (Gary Glatzmaier et Paul Roberts 1995, Weijia Kuang et Jeremy Bloxham 1997), modèles hyper-visqueux à ``2+1/2'' dimensions (Graeme Sarson et al. 1997). Ces études nécessitent des calculs très ardus. Pour les simplifier, elles sont réalisées dans des régimes de paramètres très éloignés de la Terre, et sont souvent limitées à une ou deux réalisations (sans faire varier les paramètres). Cela rend leur interprétation difficile et parfois contradictoire. Les interactions nécessaires entre les indications des simulations numériques et les études théoriques et expérimentales sont naissantes dans ce domaine. Tout cela incite bien sûr à la plus grande prudence vis à vis des modèles numériques de la dynamo terrestre, et l'on est en droit de se demander si les simulations par ordinateur peuvent faire progresser notre compréhension de ce problème. La difficulté du problème incite à la plus grande modestie quant aux objectifs de notre travail. On s'efforcera simplement de montrer dans cette thèse que, bien utilisée, et en interaction avec la théorie et l'expérience, la modélisation numérique peut, et doit, permettre de faire progresser notre compréhension des équilibres existants dans le noyau terrestre et donnant naissance au champ magnétique. Nous essaierons de montrer à travers des études de problèmes simplifiés que, pour faire progresser notre compréhension du champ magnétique terrestre à l'aide de modèles numériques, il faut s'efforcer d'approcher des caractéristiques qui font la spécificité de l'induction dans le noyau terrestre, à savoir une rotation très rapide devant les autres constantes de temps, et une diffusion du champ magnétique très efficace devant les diffusions des autres grandeurs. Nous nous intéresserons dans un premier temps aux hypothèses permettant d'établir un modèle mathématique des équilibres existants dans le noyau. Nous présenterons alors les approximations choisies pour en permettre une résolution numérique approchée. Nous appliquerons ensuite ces méthodes à deux problèmes simplifiés. Le premier, a priori assez éloigné des mécanismes pouvant exister dans le noyau, nous permettra néanmoins d'étudier avec attention les divers équilibres possibles en fonction des régimes de paramètres étudiés. Le second concerne les mouvements convectifs près du seuil ; bien que n'impliquant pas d'effets magnétiques, il constitue une étape obligée vers un modèle de géodynamo. Nous nous sommes également efforcé d'étudier les différents équilibres possibles.

Bibliographie