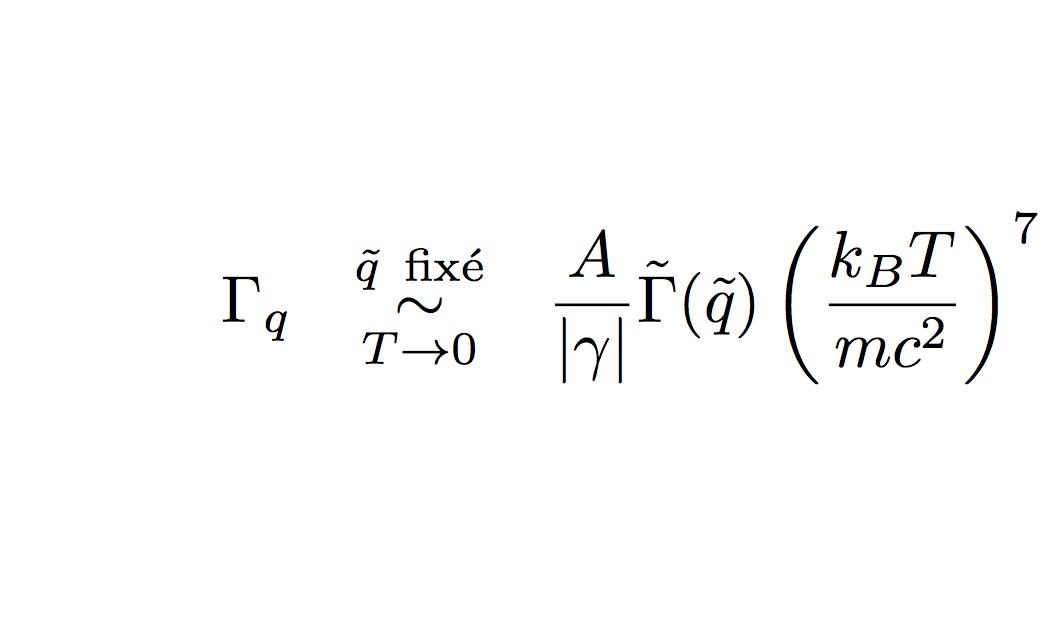À quelle vitesse un cri meurt-il dans un gaz de
phonons tristes ?
Si l'on pousse un cri dans un superfluide, comment va-t-il
s'amortir ? Dans un système isolé, l'amortissement du son
résulte d'une non-linéarité acoustique c'est-à-dire de
l'interaction entre les phonons dont l'onde est constituée. Le
mécanisme mis en jeu dépend de la forme exacte de la relation de
dispersion reliant la pulsation ωq
d'un phonon à son nombre d'onde q dans le superfluide.
Même si elle est linéaire à faible q, ωq~
cq où c est la vitesse du son, elle présente
toujours une petite courbure dont le signe détermine la nature
de l'amortissement. Si q ↦ ωq
est une fonction convexe, comme dans le cas d'école d'un
condensat de Bose-Einstein, le son s'amortit via des
processus d'interaction à trois phonons dits de Beliaev-Landau
(voir la figure 1, panneau de droite). Si q
↦ ωq
est concave (phonon triste) les processus
à trois phonons sont interdits par la
conservation de l'énergie-impulsion et l'amortissement est dû à
des processus d'ordre supérieur identifiés
par Landau et Khalatnikov en 1949 : il
s'agit de processus à quatre phonons de la forme 2 phonons ⇆ 2
phonons, provenant de l'enchaînement cohérent de deux processus
à trois phonons (voir la figure 1, panneau de gauche, qui montre
l'un des 6 diagrammes possibles). Dans
notre travail, nous avons rendu la théorie enfin quantitative en
calculant explicitement le taux d'amortissement
Γq des phonons tristes à basse
température (voir la figure 2) dans le régime faiblement
collisionnel ωqτ
coll>>1 où τ coll
est le temps de collision typique entre phonons thermiques.
L'amortissement à quatre phonons à la Landau-Khalatnikov n'a pas
encore été observé expérimentalement. Il pourrait
l'être au Laboratoire Kastler Brossel,
soit dans l'hélium 4 superfluide à haute pression, comme dans
les expériences de l'équipe "Hélium polarisé, solides et fluides
quantiques", soit dans un gaz de fermions de spin 1/2 en
interaction attractive assez faible (pas de dimères) comme sait
le produire l'équipe "Gaz de fermions froids". Dans les
deux cas, il existe un paramètre permettant d'ajuster en valeur
et en signe la courbure de la relation de dispersion : il s'agit
de la pression pour l'hélium et de la longueur de diffusion dans
l'onde s pour les fermions. Nous espérons que les
expériences pourront bientôt confirmer nos prédictions !
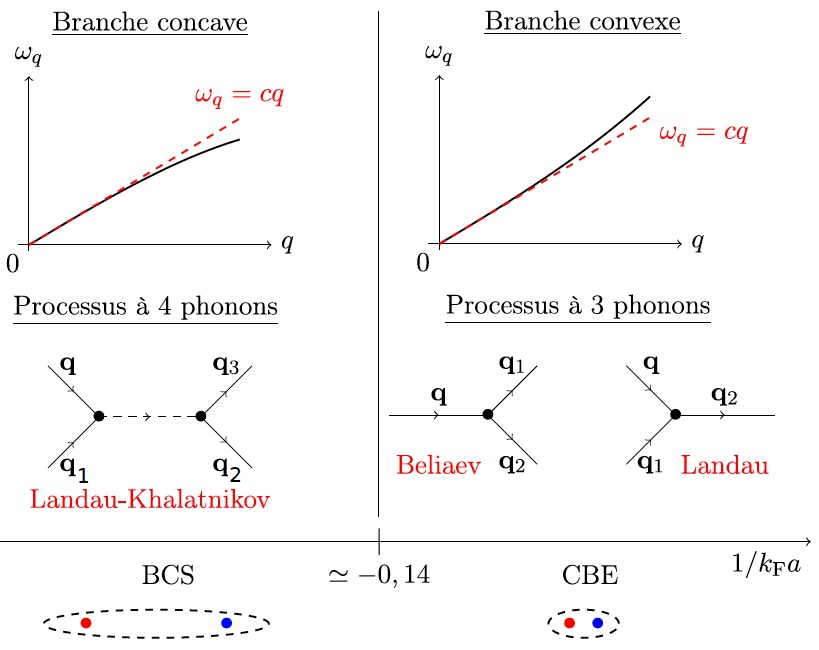
Fig.1 : Le signe de la courbure de la relation de
dispersion des phonons détermine leur processus
d'amortissement, Beliaev-Landau ou Landau-Khalatnikov (voir
texte). Dans un gaz de fermions de spin 1/2, la courbure peut
être ajustée grâce à une résonance de Feshbach, en changeant
la valeur de a donc de 1/kFa,
où kF est le nombre d'onde de Fermi
et a la longueur de diffusion dans l'onde s
entre deux fermions de spin opposé. La superfluidité du gaz
provient de la condensation de paires de Cooper d'atomes liés
(tireté entourant deux fermions de spin opposé). Dans la
limite de Bardeen-Cooper-Schrieffer (BCS) ces paires sont bien
plus grandes que la distance moyenne entre atomes, et la
relation de dispersion des phonons est concave. Dans la limite
de condensation de Bose-Einstein (CBE) les paires sont des
dimères fortement liés et la relation de dispersion est celle,
convexe, de la théorie de Bogolioubov.
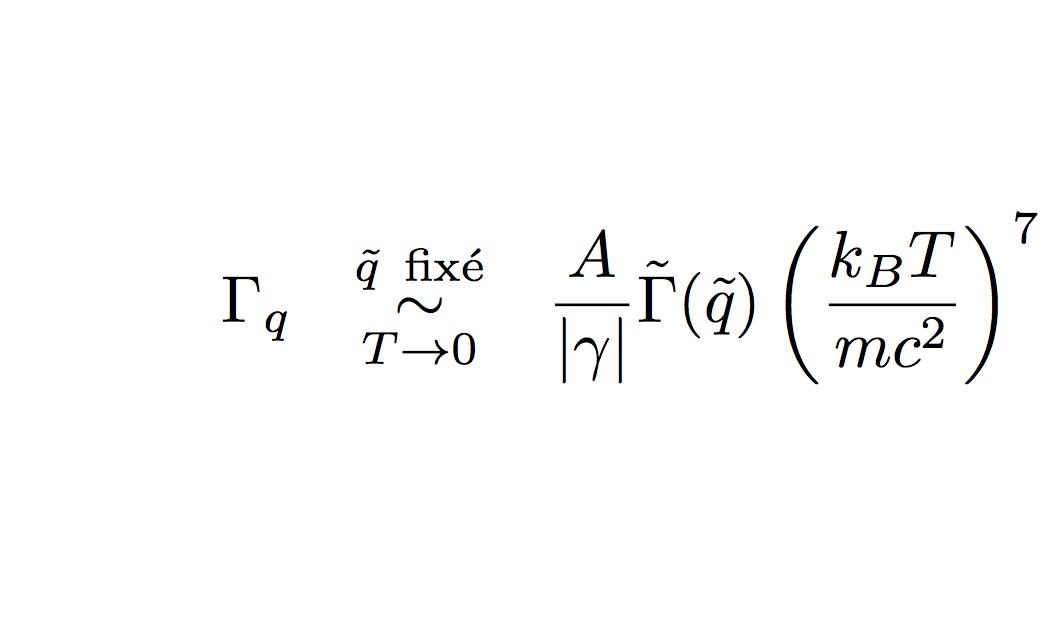
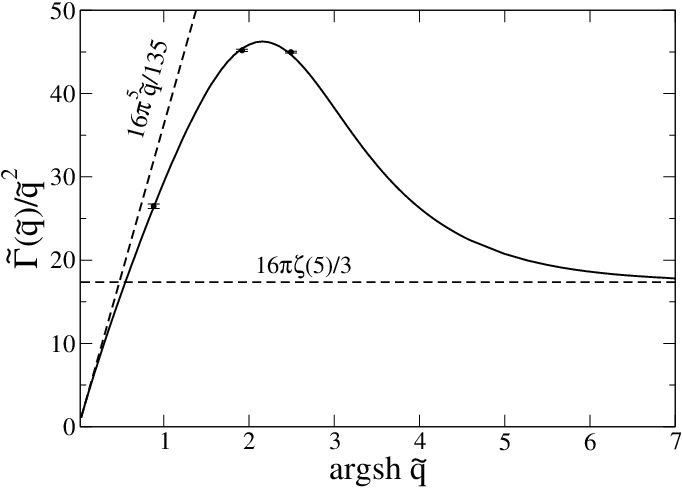
Fig.2 : Nous prédisons que le taux d'amortissement
Landau-Khalatnikov Γq d'un phonon
dans un superfluide tend vers zéro comme la puissance septième
de la température, voir l'expression sur la partie gauche de
la figure, avec en préfacteur : (i) une constante A
fonction connue de l'équation d'état du système, (ii)
au dénominateur le paramètre de courbure γ<0
de la relation de dispersion tel que
ωq
=cq[1+ (γ/8)(ℏq/mc)2+O(q4)],
(iii) une fonction universelle de
= ℏcq/kBT
représentée sur la partie droite de la figure
(après un changement de variable hyperbolique et une division
par
2).
Ici m est la masse d'une particule et c la
vitesse du son dans le superfluide. Sur le graphe, les
points avec une barre d'erreur résultent d'un calcul
numérique.
Publication
"Landau-Khalatnikov
phonon damping in strongly interacting Fermi gases", H.
Kurkjian, Y. Castin, A. Sinatra, EPL 116, 40002, 28
décembre 2016.
Contact
Alice Sinatra, alice.sinatra@lkb.ens.fr