


Next: More complicated models
Up: Results
Previous: Organized behavior
The results of the mean field approach were obtained from
a differential equation modeling a discrete time algorithm.
They are valid when the changes at each step of the
algorithm can be considered as small. Variables 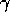 and
and  thus have to be small, which is true for the simulation results
given in figures 1 and 2. One of the features noticed by
observing on-line the motion of individual buyers on the simplex plots
is that agents sometimes move "backward" towards shops
which are not the shops that they prefer in the ordered regime. But
since for most of the time they move towards preferred shops,
these "infidelities" never make them change shops and preferences
permanently. They commit "adultery", but do not "divorce".
thus have to be small, which is true for the simulation results
given in figures 1 and 2. One of the features noticed by
observing on-line the motion of individual buyers on the simplex plots
is that agents sometimes move "backward" towards shops
which are not the shops that they prefer in the ordered regime. But
since for most of the time they move towards preferred shops,
these "infidelities" never make them change shops and preferences
permanently. They commit "adultery", but do not "divorce".
When variables 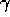 and
and  are increased, infidelities have
more important consequences, and customer might change fidelity:
they may "divorce" one shop for another one. Indeed increasing
are increased, infidelities have
more important consequences, and customer might change fidelity:
they may "divorce" one shop for another one. Indeed increasing  results in larger steps taken by customers on the simplex,
which might make them go from one corner neighborhood
to another one in a few time steps. In fact the probability of
a given path on the simplex varies as the product of probabilities
of individual time steps: when fewer steps are needed the probability
that the process will generate such changes
becomes higher. Because of the exponential growth of
time of the "divorce" process with respect to
results in larger steps taken by customers on the simplex,
which might make them go from one corner neighborhood
to another one in a few time steps. In fact the probability of
a given path on the simplex varies as the product of probabilities
of individual time steps: when fewer steps are needed the probability
that the process will generate such changes
becomes higher. Because of the exponential growth of
time of the "divorce" process with respect to  , a small
change in relevant parameters,
, a small
change in relevant parameters,  or
or 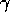 results in a switch from a no-divorce regime to a divorce regime.
Divorces are observable on-line on the simplex plots
and also by examining the evolution of the number of customers as
a function of time.
results in a switch from a no-divorce regime to a divorce regime.
Divorces are observable on-line on the simplex plots
and also by examining the evolution of the number of customers as
a function of time.
weisbuch
Mon Feb 10 13:26:18 GMT+0100 1997
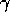 and
and  thus have to be small, which is true for the simulation results
given in figures 1 and 2. One of the features noticed by
observing on-line the motion of individual buyers on the simplex plots
is that agents sometimes move "backward" towards shops
which are not the shops that they prefer in the ordered regime. But
since for most of the time they move towards preferred shops,
these "infidelities" never make them change shops and preferences
permanently. They commit "adultery", but do not "divorce".
thus have to be small, which is true for the simulation results
given in figures 1 and 2. One of the features noticed by
observing on-line the motion of individual buyers on the simplex plots
is that agents sometimes move "backward" towards shops
which are not the shops that they prefer in the ordered regime. But
since for most of the time they move towards preferred shops,
these "infidelities" never make them change shops and preferences
permanently. They commit "adultery", but do not "divorce".
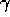 and
and  are increased, infidelities have
more important consequences, and customer might change fidelity:
they may "divorce" one shop for another one. Indeed increasing
are increased, infidelities have
more important consequences, and customer might change fidelity:
they may "divorce" one shop for another one. Indeed increasing  results in larger steps taken by customers on the simplex,
which might make them go from one corner neighborhood
to another one in a few time steps. In fact the probability of
a given path on the simplex varies as the product of probabilities
of individual time steps: when fewer steps are needed the probability
that the process will generate such changes
becomes higher. Because of the exponential growth of
time of the "divorce" process with respect to
results in larger steps taken by customers on the simplex,
which might make them go from one corner neighborhood
to another one in a few time steps. In fact the probability of
a given path on the simplex varies as the product of probabilities
of individual time steps: when fewer steps are needed the probability
that the process will generate such changes
becomes higher. Because of the exponential growth of
time of the "divorce" process with respect to  , a small
change in relevant parameters,
, a small
change in relevant parameters,  or
or 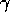 results in a switch from a no-divorce regime to a divorce regime.
Divorces are observable on-line on the simplex plots
and also by examining the evolution of the number of customers as
a function of time.
results in a switch from a no-divorce regime to a divorce regime.
Divorces are observable on-line on the simplex plots
and also by examining the evolution of the number of customers as
a function of time.