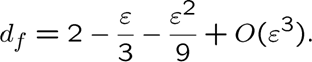A loop-erased random walk with its shadow,
courtesy of
Michel Bauer and Denis Bernard
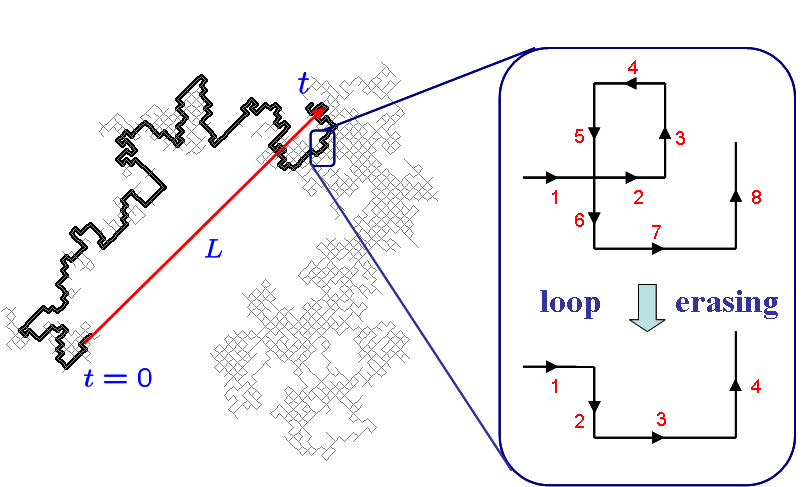
The loop-erased random walk (LERW) was introduced by Lawler (1980) as a mathematically more tractable object than the self-avoiding walk (SAW). Nowadays, the LERW has numerous applications in combinatorics, self-organized criticality, conformal field theory and SLE. The SAW is defined as the uniform measure on all non-self-intersecting walks, and is well treatable by field-theoretic methods. The LERW is defined as the trajectory of a random walk in which any loop is erased as soon as it is formed:

|
The number of steps t
(not counting the erased loops) it takes to reach the distance
L scales as