L'approximation numérique
L'approximation numérique
Dans certains cas simples, on sait calculer analytiquement les solutions exactes de ces équations (c'est à dire résoudre <<à la main>> avec les outils de l'analyse), mais les calculs sont en général bien trop longs pour un cas réaliste ; et surtout, dans beaucoup de cas, on ne sait pas le faire, et il faut alors utiliser des approximations numériques.
L'étude théorique des modèles mathématiques se ramène alors à deux questions fondamentales. Existe-t-il une solution au problème, et si oui cette solution est elle unique ? Si le problème n'a pas de solution, il est inutile de perdre son temps à chercher à en construire une. S'il en possède plusieurs, il faudra se donner des conditions supplémentaires de façon à en sélectionner une seule ; celle qui nous intéresse.
Si l'équation admet plusieurs solutions cela peut être dû au fait que l'on a oublié d'y inclure une partie des contraintes du problème physique, mais cela peut être aussi dû à l'existence effective de plusieurs solutions physiques. Ceci est très facile à comprendre sur l'exemple du <<flambement de la poutre>>. Si nous prenons une baguette et que nous appuyons sur ses deux extrémités dans la direction de son axe que se passe-t-il ?
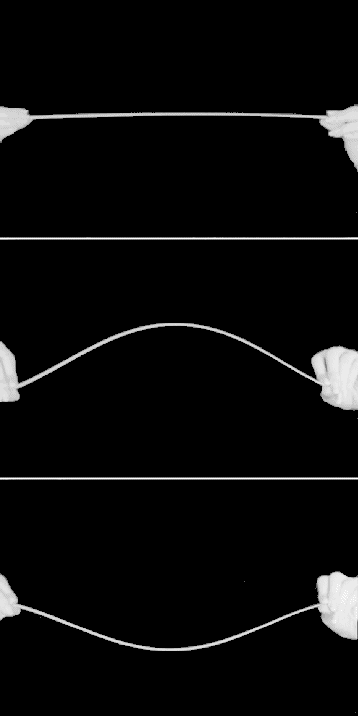
Figure 8 : Une poutre encastrée soumise
à compression, peut <<flamber>> vers le haut ou
vers le bas.
Jusqu'à une certaine force il ne se passe rien. Puis si nous continuons à appuyer de plus en plus fort, d'un seul coup la baguette se courbe soit vers le haut, soit vers le bas ; on dit qu'elle <<flambe>>. En fait, lorsque la force appliquée augmente, la solution rectiligne (où la baguette est droite) devient instable (à la manière d'une pièce de monnaie posée sur la tranche). C'est-à-dire que la baguette peut rester dans cette position, mais la moindre perturbation la fera <<flamber>> dans un sens ou dans l'autre. Ce passage d'un état avec une solution stable vers un état avec deux solutions stables et une solution instable, s'appelle une bifurcation.
Pour une force assez grande, ce problème admet donc en plus de l'équilibre instable, deux solutions possibles d'équilibre stable. Une vers le haut, l'autre vers le bas... Voici donc un phénomène physique dont on peut attendre que la résolution de son équation admette plusieurs solutions.
Au problème d'existence et d'unicité de la solution s'ajoute la question de savoir si la solution varie continuement en fonction des données (les données regroupent l'ensemble des conditions initiales : forme, forces exercées,... et les éventuelles variations en temps de ces grandeurs) ; c'est-à-dire, si l'on change à peine les données du problème, la solution va-t-elle changer peu ou beaucoup ? Dans le cas où l'équation est <<gentille>> sa solution variera continuement en fonction des données (c'est le cas de la membrane : si l'on augmente à peine la taille des bâtonnets, la membrane monte à peine plus haut), mais il y a des problèmes, dits mal conditionnés ou mal posés, où une petite différence dans les paramètres induit un comportement totalement différent de la solution (c'est le cas des phénomènes dits <<chaotiques>>). Dans ces cas, même si l'on connaît l'existence et l'unicité de la solution, la moindre erreur commise au cours du calcul a une répercussion considérable sur la solution...
Un problème mathématique est dit bien posé au sens d'Hadamard s'il répond favorablement aux trois questions que nous venons d'aborder, c'est-à-dire s'il admet une solution, qui est unique, et dépendant continuement des données.
L'approximation numérique
Document réalisé par Emmanuel Dormy
L'énigme du Sphinx
Retour à ma "home page"