![]() Rappels d'analyse fonctionnelle
Rappels d'analyse fonctionnelle
C'est à l'aide de ces outils (dérivée et dérivées partielles) que se définissent ces <<énigmes du Sphinx>> que sont les équations aux dérivées partielles . Ce n'est pas un hasard, ni un phénomène surnaturel, si les équations de la physique utilisent ces notions de dérivées (de pente locale) ; en effet la physique regorge de notions qui sont les dérivées les unes des autres. Ainsi l'accélération d'une voiture n'est en fait que la dérivée de sa vitesse (plus elle accélère, plus sa vitesse augmente <<vite>>, c'est-à-dire plus la pente de la vitesse par rapport au temps est grande), et la vitesse elle même n'est autre que la dérivée de la position...
Passons à un exemple de ces énigmes : <<Quelle est la fonction dont la dérivée vaut zéro partout ?>>. Ce la signifie que la pente est partout nulle, c'est-à-dire qu'en chaque point, on ne monte ni ne descend lorsque l'on avance. La réponse à cette énigme est donc la droite horizontale.
A peine plus compliqué <<Quelle est la fonction dont la dérivée vaut 1 partout ?>> En suivant le même raisonnement, lorsque j'avance d'un pas je monte d'un pas, il s'agit donc d'une droite inclinée à 45 degrés avec l'horizontale.
<<Quelle est la fonction dont la pente est partout égale à la fonction elle-même ?>> Les choses sérieuses commencent ...
Une première approche, qui est assez classique en maths, c'est de se ramener au problème précédent. Supposons que la fonction soit nulle... On se ramène alors à la première énigme que nous avons regardée. La fonction horizontale qui vaut zéro partout est bien de pente nulle, et elle est donc solution de notre problème...
Oui, mais si je pars d'un point non nul, puis-je quand même construire une fonction qui satisfasse notre énigme ?
Essayons d'en dessiner une ! Nous allons procéder de manière approchée pour avoir une idée de la solution ( cf figure 6).
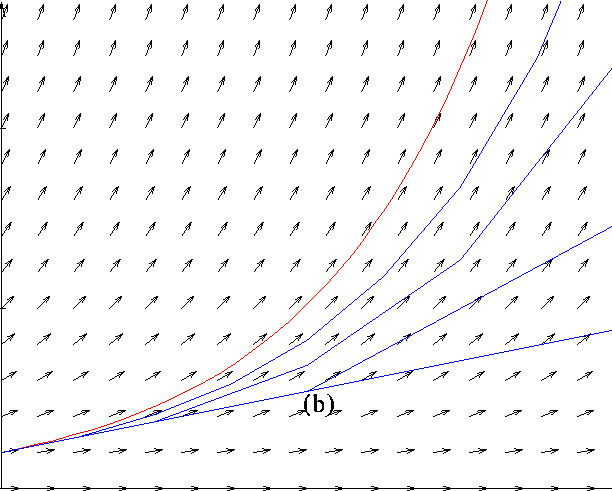
Figure 6 : Construction de l'exponentielle.
On peut représenter sur le plan des flèches qui indiquent la pente que doit avoir la solution pour satisfaire l'énigme. Celle-ci dépend bien sur de l'altitude. Le problème est donc de trouver une trajectoire qui passe par (a), et qui soit partout tangente aux flèches.
Donnons-nous un point non nul (a) ; si nous comprenons les termes de l'énigme, la valeur en ce point nous donne également la pente de la fonction en ce point. La droite passant par (a) et dont la pente est ainsi définie constitue donc une approximation grossière de la solution. Si nous nous arrêtons en un point (b) de cette droite, nous sommes obligés de constater que nous ne satisfaisons pas aux termes de l'énigme.
Si nous étions bien en un point de la solution, notre pente devrait être plus grande, puisque nous sommes plus haut. Nous avançons donc avec ce nouveau cap, donné par la valeur en (b). On obtient alors une ligne brisée de deux segments, qui est sans doute plus proche de la solution que la droite initiale.
Pour obtenir une meilleur approximation, on peut répeter l'opération avec un pas deux fois plus petit (le pas est la distance entre (a) et (b)), on obtient alors une ligne brisée de quatre segments. Cette ligne n'est pas la solution de notre problème, mais elle s'en approche. On obtient une ligne de huit segments, avec un pas encore deux fois plus petit. Et ainsi de suite...
Et plus nous diminuons le pas, plus nous constatons que notre ligne brisée semble se rapprocher d'une courbe. On obtient une approximation toujours plus fine de la solution, que ceux qui la connaissent peuvent identifier comme une croissance exponentielle.
Cette méthode est due à Leonhard Euler, un mathématicien suisse du XVIIIème siècle. Nous n'avons pas réellement résolu l'équation, mais nous connaissons une allure approchée de sa solution. On constate, comme pour la membrane, que plus il y a de points, plus la solution est <<bonne>>.
Quel est l'intérêt que l'on peut bien trouver à ces énigmes ? Il dépasse le plaisir des mathématiques pures.
Ainsi Sir Isaac Newton a observé que <<la vitesse de refroidissement d'un corps quelconque dans l'air est proportionnelle à la différence entre la température de ce corps et l'air ambiant>>.
Si nous plongeons un corps dans de l'air à zéro degré, l'équation devient : <<la vitesse de refroidissement d'un corps quelconque dans de l'air à zéro degré est proportionnelle à la température de ce corps>>. Donc si nous cherchons à connaître l'évolution de la température au cours du temps, nous voyons que l'équation à résoudre est grosso modo la même que celle qui nous intéresse actuellement. Une version simplifiée de l'équation d'évolution de la température de ce corps peut s'exprimer ainsi : <<Quelle est la fonction dont la pente est partout opposée à la fonction elle même ?>>. Si nous appliquons la même méthode que précédemment pour résoudre cette équation nous obtenons une solution, c'est-à-dire une relation entre la température et le temps, dont l'allure est la symétrique de l'exponentielle ( cf figure 7).
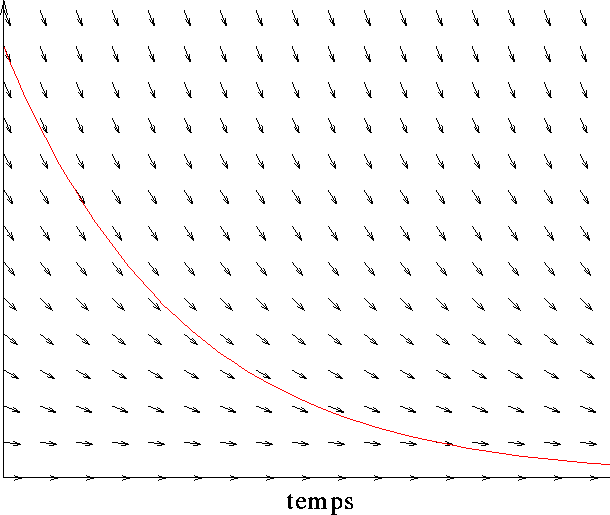
Figure 7 : Evolution de la température d'un corps plongé dans un
milieu plus froid que lui.
C'est-à-dire que plus la différence de température est grande entre le corps et l'air, plus le corps va se refroidir vite.
On remarque au passage que ces énigmes mettent souvent en cause des variations tant spatiales (variations en espace) que temporelles (évolution en temps), le temps n'étant en mathématiques qu'une dimension (un paramètre) possible.
Si je vous demandais enfin <<Quelle est la fonction de deux variables (c'est-à-dire la colline de tout à l'heure) dont la dérivée seconde (la dérivée de la dérivée) dans une direction ajoutée à la dérivée seconde dans l'autre est nulle ?>>, vous me laisseriez sans doute là avec mes questions tordues, et vous auriez bien raison !
C'est pourtant là l'équation de notre membrane. L'on comprend donc l'intérêt de traiter le problème à l'aide d'une machine !
Je voudrais insister ici sur un point important, et combattre une idée reçue trop courante : mettre le problème en équation, ce n'est pas le résoudre. C'est le formaliser. En d'autres termes ce n'est pas parce qu'on connaît l'équation d'un phénomène que ce phénomène est connu et compris. On ne connait que l'énigme à laquelle il va falloir répondre. Il est d'ailleurs frappant que bien que ces équations aux dérivées partielles (qui traduisent des relations locales) soient en général relativement simples, leurs solutions globales soient souvent très complexes.
![]() Rappels d'analyse fonctionnelle
Rappels d'analyse fonctionnelle
Document réalisé par Emmanuel Dormy