


Next: Preference coefficientslearning
Up: The simplest Model
Previous: The simplest Model
The buyers will wish to buy a quantity from sellers
given the price per unit p which is proposed
and are able to resell in their own local market where they face a
demand function 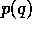 , which determines the relationship between the
price they obtain and the quantity q that they bring to the local
market. Let us suppose in order to simplify matters
that
, which determines the relationship between the
price they obtain and the quantity q that they bring to the local
market. Let us suppose in order to simplify matters
that 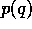 is known by the buyers, is the same for all buyers
and that it is a simple function of q such as:
is known by the buyers, is the same for all buyers
and that it is a simple function of q such as:

The particular choice of the function 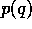 is of no importance and is made to facilitate calculations and to
provide clear benchmarks. For the model any monotonic decreasing
function would suffice. The buyer's profit is then:
is of no importance and is made to facilitate calculations and to
provide clear benchmarks. For the model any monotonic decreasing
function would suffice. The buyer's profit is then:
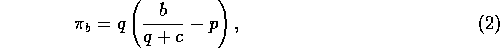
We suppose then that the buyer knows the demand curve he faces
and is thus able to compute
the quantity that will maximise his profit for
a given price p proposed by the seller.
This quantity is:

We make similar assumptions for the sellers,
in particular that they know the behavior of buyers described by
the three equations above, and they can therefore maximize their own profit
per transaction:
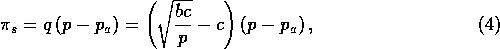
with respect to the price p that they charge to the buyers, where
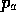 is the price at which the sellers themselves purchase the fish.
(Since the price p which maximises equation 4 is the solution of
a third degree equation, its expression is rather complicated
and not given here).
is the price at which the sellers themselves purchase the fish.
(Since the price p which maximises equation 4 is the solution of
a third degree equation, its expression is rather complicated
and not given here).
In order to simplify assumptions as much as possible,
let us suppose that:
-
All sellers propose a single price p to all their customers.
-
Customers choose one shop everyday. As long as the shop has supplies,
they are offered goods
at price p; customers then purchase q given by equation 3.
Whether they do get supplies when they visit the shop depends upon
the time they visit the shop, which is randomly chosen in the simulations.
It also depends on how much the sellers bring each day to the market.
-
Each day sellers bring a fish quantity Q in relation
to
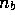 , the expected number of customers for that day.
In the simplest version of the model, this fish quantity
is
, the expected number of customers for that day.
In the simplest version of the model, this fish quantity
is 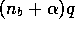 , where
, where 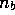 is the number of customers who
visited yesterday and
is the number of customers who
visited yesterday and 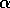 a constant extra fraction brought to attract for
the future extra customers that could show up.
a constant extra fraction brought to attract for
the future extra customers that could show up.



Next: Preference coefficientslearning
Up: The simplest Model
Previous: The simplest Model
weisbuch
Mon Feb 10 13:26:18 GMT+0100 1997
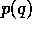 , which determines the relationship between the
price they obtain and the quantity q that they bring to the local
market. Let us suppose in order to simplify matters
that
, which determines the relationship between the
price they obtain and the quantity q that they bring to the local
market. Let us suppose in order to simplify matters
that 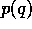 is known by the buyers, is the same for all buyers
and that it is a simple function of q such as:
is known by the buyers, is the same for all buyers
and that it is a simple function of q such as:

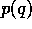 is of no importance and is made to facilitate calculations and to
provide clear benchmarks. For the model any monotonic decreasing
function would suffice. The buyer's profit is then:
is of no importance and is made to facilitate calculations and to
provide clear benchmarks. For the model any monotonic decreasing
function would suffice. The buyer's profit is then:
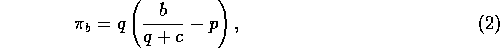

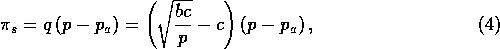
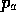 is the price at which the sellers themselves purchase the fish.
(Since the price p which maximises equation
is the price at which the sellers themselves purchase the fish.
(Since the price p which maximises equation 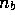 , the expected number of customers for that day.
In the simplest version of the model, this fish quantity
is
, the expected number of customers for that day.
In the simplest version of the model, this fish quantity
is 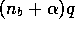 , where
, where 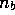 is the number of customers who
visited yesterday and
is the number of customers who
visited yesterday and 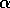 a constant extra fraction brought to attract for
the future extra customers that could show up.
a constant extra fraction brought to attract for
the future extra customers that could show up.