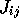 :
:
A generalization of this approach to our problem is to write
a differential equation describing the time evolution
of one 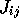 :
:
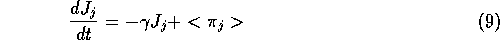
where  is the average profit, related to
is the average profit, related to  the profit
obtained from one actual transaction as follows:
the profit
obtained from one actual transaction as follows:
where the fraction represent the probability of that buyer i
visits seller j and 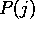 is the probability that the shop still
has goods to sell when he comes.
We suppress here the i index corresponding to the buyer.
In other words,
the above set of equations couples the evolution of all the
is the probability that the shop still
has goods to sell when he comes.
We suppress here the i index corresponding to the buyer.
In other words,
the above set of equations couples the evolution of all the 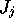 .
Equilibrium values are obtained by equating the derivatives to zero.
.
Equilibrium values are obtained by equating the derivatives to zero.
Let us consider the simplest case of two shops and to further
simplify computation,
let us suppose, for the moment, that 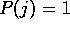 , which happens when buyers always find what they require at the seller they visit.
The equilibrium relations
are in this case:
, which happens when buyers always find what they require at the seller they visit.
The equilibrium relations
are in this case:
Subtracting equation 12
from equation 11, we see that the
difference between the two fidelities,
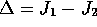 , obeys the following implicit equation:
, obeys the following implicit equation:
The right hand side of the equation is in fact the hyperbolic tangent of
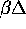 /2 . The above equation has either one or three solutions according
to the slope
of the hyperbolic tangent at the origin.
/2 . The above equation has either one or three solutions according
to the slope
of the hyperbolic tangent at the origin.
By developing the hyperbolic tangent in series for
small values of 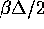 , it is easily seen that for:
, it is easily seen that for:

there is only one solution 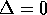 and
and 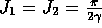 .
Since in this case the average
.
Since in this case the average 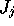 are small and equal,
the probabilities of visiting
either shop simply fluctuate. No order is observed.
are small and equal,
the probabilities of visiting
either shop simply fluctuate. No order is observed.
In the opposite situation, when 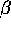 is above
is above
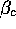 , the zero solution is unstable
and one obtains two symmetrical solutions
where one fidelity is larger than the other one by a factor
which is exponential
in
, the zero solution is unstable
and one obtains two symmetrical solutions
where one fidelity is larger than the other one by a factor
which is exponential
in 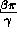 .
The transition between the two regimes is abrupt.
A development in series
of the hyperbolic tangent around 0 shows that the larger fidelity increases
in
.
The transition between the two regimes is abrupt.
A development in series
of the hyperbolic tangent around 0 shows that the larger fidelity increases
in 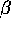 as the square root of the distance to the transition:
as the square root of the distance to the transition:
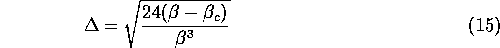
Fidelities are then continuous across the transition, but they rise (or decrease) with an infinite slope at the transition. Expression (14) can be generalized to any number n of shops:

The above analysis shows that as long as the mean field approximation
remains valid, the qualitative behavior of the dynamics, ordered or
disordered, only depends on one parameter,
namely the ratio between 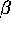 and
and 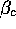 . All other parameters
simply change the scale of profits, prices, numbers of shops and
customers. The time scale of learning depends on
. All other parameters
simply change the scale of profits, prices, numbers of shops and
customers. The time scale of learning depends on 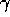 :
order, when achieved, is reached faster for larger values of
:
order, when achieved, is reached faster for larger values of 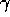 .
.
The three parameters  ,
, 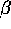 and
and 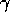 control the transition.
Sellers set prices and thus determine
control the transition.
Sellers set prices and thus determine  , the buyers' profit.
The buyers characteristics determine
, the buyers' profit.
The buyers characteristics determine
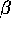 and
and 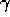 . We might reasonably assume that
agents are not all identical and that their characteristic parameters
vary. Prices may not vary widely since there is competition
between sellers. On the other hand, memory (characterised by
. We might reasonably assume that
agents are not all identical and that their characteristic parameters
vary. Prices may not vary widely since there is competition
between sellers. On the other hand, memory (characterised by 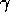 )
and discrimination rate (characterised by
)
and discrimination rate (characterised by 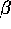 ) might differ between buyers.
If these variations are large enough, we might expect to observe two distinct
classes of buyers: faithful buyers, who most of the time visit
the same shop, would be those whose parameters
are such that
) might differ between buyers.
If these variations are large enough, we might expect to observe two distinct
classes of buyers: faithful buyers, who most of the time visit
the same shop, would be those whose parameters
are such that 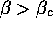 , while searchers with parameters
such that
, while searchers with parameters
such that 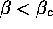 would wander from shop to shop.Indeed
precisely this sort of "division of labour" is observed on the Marseille
fish market which was the empirical starting point for this paper.
would wander from shop to shop.Indeed
precisely this sort of "division of labour" is observed on the Marseille
fish market which was the empirical starting point for this paper.
Let us also note that the predicted nonhomogeneous distribution of behavior is a dynamical feature which is very different from the phase transitions observed when agents use information from the behavior of other agents through social interactions (Follmer 1974, Arthur and Lane 1993, Brock and Durlauf 1995, Orlean 1995), rather than from their past experience as in this model. In the case of social interactions, order or disorder is a characteristic of the market, and all agents share the same behavior, either ordered or disordered depending upon average values of the parameters.