La modélisation

Introduction aux Expériences Numériques

Déformation d'une membrane élastique

Etudions le comportement d'une membrane élastique soumise à une déformation. Pour analyser un tel phénomène, l'approche classique passe par la réalisation d'une maquette, puis de <<manips>> où l'on déforme celle-ci à l'aide d'une baguette ( cf photo, figure 1).

  
Figure 1 : Déformation d'une membrane élastique.

Pour réaliser une simulation numérique de ce phénomène, il faut surmonter quelques difficultés. Notre objectif est de connaître sans réaliser de <<manip>> la forme que va prendre la membrane. Or cette membrane est bien sûr constituée d'une infinité de points. Pour calculer numériquement avec un ordinateur la position de cette infinité de points, il faudrait un temps infini et une mémoire infinie... Il faut donc ramener le problème à un nombre fini d'inconnues et sa résolution à un nombre fini de calculs. En fait on va chercher une approximation de la position en un certain nombre de points. On va regrouper ces points en triangles, et supposer que la solution varie linéairement sur chaque triangle.

Un exemple de résolution est donné figure 2. Chaque ligne (a, b, c) correspond à une simulation, vue du dessus à gauche et en perspective à droite. Du haut en bas, le nombre de triangles augmente à chaque simulation. On constate évidemment que la qualité de la solution augmente avec le nombre de triangles.

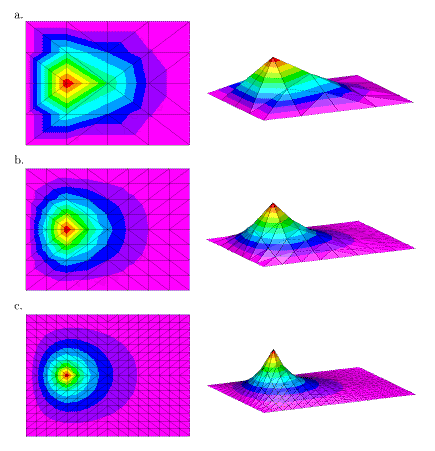
Figure 2 : Simulation numérique d'une membrane élastique. La qualité du résultat augmente avec le nombre de triangles utilisés. On observe l'anisotropie numérique liée à l'usage d'une grille régulière, et la mauvaise répartition du phénomène physique.

On peut cependant faire quelques remarques importantes. La première, est que en contrepartie de cette amélioration du résultat, l'augmentation du nombre de triangles entraîne une augmentation du temps de calcul nécessaire à la résolution du problème. A chaque étape, on a multiplié par huit le nombre de triangles, et par 64 le temps de calcul. On ne peut donc continuer à accroître indéfiniment le nombre de triangles, sous peine de devoir attendre très longtemps le résultat.

D'autre part, on constate que la répartition régulière de triangles que nous utilisons n'est pas très judicieuse. En effet, dans notre cas, et c'est souvent ainsi, le phénomène que l'on étudie est mal réparti dans l'espace ; c'est-à-dire qu'il y a des régions où il se passe quelque chose (où le déplacement est important) et des régions où il ne se passe presque rien. On peut donc augmenter la qualité du résultat numérique sans augmenter le nombre de triangles, simplement en répartissant les points de calcul de sorte qu'ils soient plus serrés là où il se passe quelque chose.

Enfin, on constate que si la solution devient globalement de plus en plus lisse, la forme de la grille (les triangles) reste visible près de la baguette (point singulier), ceci malgré l'augmentation du nombre de triangles. Ce phénomène d'influence de la forme de la grille sur la solution s'appelle l' anisotropie numérique. Une solution possible à ce problème serait de rendre la grille irrégulière, afin qu'elle n'ait pas de forme particulière.

Fort de toutes ces remarques, nous décidons donc d'utiliser une grille irrégulière (où tous les triangles sont différents), et adaptée au problème (c'est-à-dire avec plus de triangles là où la déformation est importante).

On constate alors sur la figure 3 que la première simulation, avec sensiblement le même nombre de triangles (512) que la dernière simulation de la figure 2, offre une meilleure approximation de la solution. Enfin, si l'on augmente encore le nombre de triangles (dernière ligne), on obtient un résultat très proche de la réalité physique, et on ne distingue presque plus les triangles utilisés pour le calcul (leurs contours ont été volontairement supprimés sur cette image).

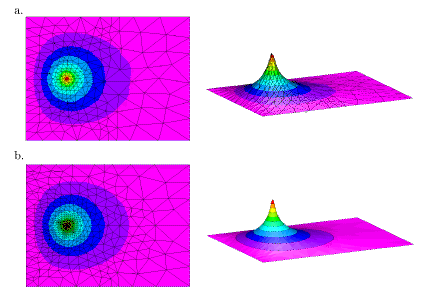
Figure 3 : Avec une grille adaptative, on arrive à un résultat très proche de la réalité physique.

La modélisation

Introduction aux Expériences Numériques

Retour à ma "home page"