On connaît aujourd'hui beaucoup d'équations aux dérivées partielles dont on ne sait pas calculer analytiquement la solution, et dont on ne sait même pas si elle existe, et si elle est unique.
Dans certains cas on sait démontrer l'existence et l'unicité de la solution (c'est par exemple le cas de la membrane, si elle est assez régulière). Dans d'autres cas, on ne sait encore rien dire de la solution théorique, ce qui rend l'interprétation des simulations numériques très difficile.
Tout ceci constitue le thème de nombreuses recherches mathématiques actuelles en analyse (P.L.Lions a reçu la Médaille Fields en 1994 pour ses travaux dans ce domaine), ainsi qu'en techniques numériques.
L'un des avantages notoires de la simulation numérique sur les expériences traditionnelles est la différence de coût.
Les simulations numériques (on parle parfois en aero ou hydrodynamique de soufflerie numérique) coûtent en général beaucoup moins cher que les essais correspondants (moteurs de voitures, ailes d'avions, coques de bateau...), ceci bien que les programmes coûtent cher, ainsi que l'usage des super-calculateurs. Mais, dans beaucoup de domaines, elles sont devenues complémentaires des essais sans pour autant les remplacer (on peut se référer à Les défis aérodynamiques des avions de combat par J.D. Marion dans la Revue du Palais de la Découverte, vol.23, no 222).
L'efficacité des simulations numériques est souvent spectaculaire. On peut voir figure 9 un test de collision sur une voiture lancée à 55 km/h, ce test est réalisé d'abord de façon classique, puis simulé numériquement. L'accord entre les deux images est saisissant. Cette simulation nécessité plus de trois heures de calculs sur un super-ordinateur CRAY Y-MP. On peut noter que les éléments utilisés pour le calcul ont été adaptés pour être plus denses là où la déformation est importante.


Figure 9 : Test de collision à 55 km/h, et simulation numérique.
Mais revenons à notre membrane. Quelle serait sa forme si, au lieu d'être attachée sur les quatre côtés, elle ne l'était que sur deux d'entre eux ?
L'expérimentateur qui se pose cette question n'a plus qu'à découper sa membrane, ou à construire une autre maquette ; alors qu'un programme de simulation numérique ne demande bien souvent qu'une petite modification ( cf figure 10).
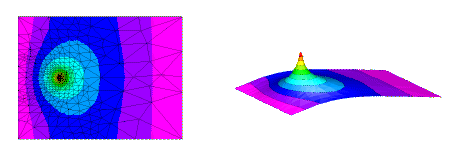
Figure 10 : La même membrane avec seulement deux bords attachés.
Sans doute encore plus important que le problème du coût, elles permettent de lire toutes les valeurs des différents paramètres sans perturber l'experience. Dans une expérience en labo classique, pour mesurer la variation de pression due au passage d'une onde, on utilise une sonde, qui va perturber l'onde, et donc les mesures que l'on pourra en faire par la suite. Lors d'une simulation numérique on a un accès direct aux valeurs sans perturber le phénomène observé. On peut également modifier à loisir les paramètres et essayer différentes possibilités mêmes non physiques pour observer <<ce qui se passerait si...>>
Outre la compréhension de phénomènes physiques par une étude fine de leur comportement, l'un des attraits majeurs des simulations numériques est de permettre à moindres frais de réaliser plusieurs fois de suite la même expérience en faisant varier l'un ou l'autre de ces paramètres et d'en observer l'effet. On peut par exemple observer l'amélioration aérodynamique apportée par la variation de la forme d'une aile d'avion. Compte tenu du nombre de profils d'ailes possibles on imagine le travail que demanderait la construction de maquettes pour l'essai systématique de toutes les possibilités. Même numériquement, il est énorme, d'où la nécessité d'envisager une approche scientifique du problème. C'est l'optimisation de forme (science assez récente, environ 1950), dont l'objet est de déterminer comment modifier des paramètres contrôlant un modèle pour en obtenir une caractéristique optimale.
Il faut cependant se garder de certains pièges : la simulation numérique doit intervenir en complément des expériences traditionnelles (qui servent de validation). Il faut rester conscient que l'on ne manipule que des approximations, ce qui pose le problème de l'adéquation avec le monde réel. Comme on l'a dit précédemment, un modèle repose en fait sur une série d'hypothèses, et n'est valable que tant que ces hypothèses le sont.
Ainsi, l'on peut très bien simuler numériquement le flambement de la poutre, dont nous avons déja parlé. La figure 11 représente les simulations correspondantes aux photos de la figure 8. Le modèle numérique y apparaît comme tout-à-fait valable.
Mais, si l'on augmente la force exercée et que l'on s'intéresse aux deux solutions stables, on s'aperçoit vite que le modèle numérique continue à flamber, là où une vraie poutre se serait sans doute cassée (cf figure 12). Et, en exagérant vraiment, on finit même par obtenir une poutre qui s'auto-intersecte (cf figure 13) ! Ceci met bien en évidence la notion de domaine de validité d'un modèle, et souligne les dangers d'une trop grande confiance en un résultat purement numérique.
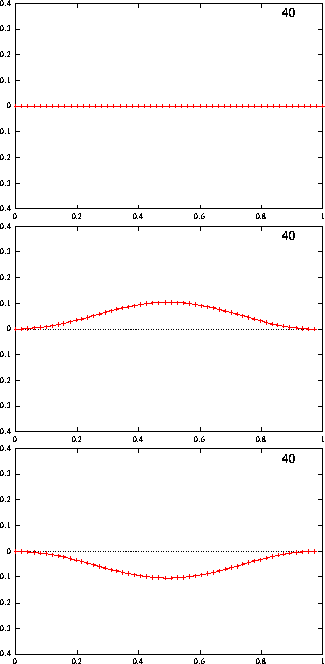
Figure 11: Simulation d'une poutre encastrée qui <<flambe>>. En haut,
la solution rectiligne, qui devient instable ; en dessous, les deux
autres solutions stables. On représente ici par des croix les 50
points de calculs. Ces croix sont supprimées sur les figures
suivantes pour mettre en évidence la qualité de l'approximation.
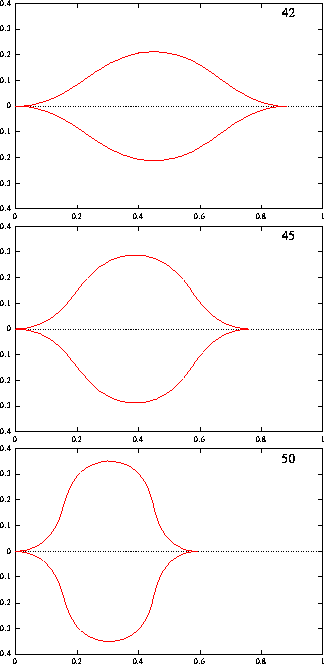
Figure 12 : Même modèle, en augmentant la force exercée. On
représente à présent sur la même image les deux solutions
stables.
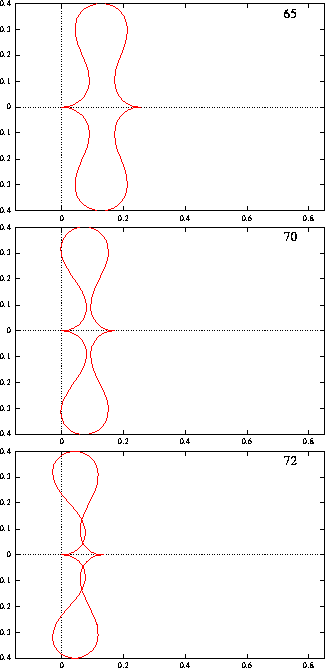
Figure 13 : Si l'on augmente encore la force exercée, on sort
clairement des limites du modèle, qui ne correspond plus alors à
la réalité physique. En particulier, sur la dernière
image, la poutre "immatérielle" s'auto-intersecte !
L'auteur tient à remercier Jean Brette, Claude Basdevant, Vincent
Courtillot et Albert Tarantola pour leur aide précieuse lors de la
préparation comme de la relecture de ce manuscrit.
Les simulations d'accident de voiture ont étés réalisées par
Thomas Frank et Karl Gruber de Mercedes-Benz AG sur ordinateurs CRAY.
Les simulations de la membrane ont étés réalisées à l'aide
d'un court programme écrit par l'auteur, utilisant la librairie PLTMG,
de Randolph E. Bank.
Les simulations de flambement de poutre ont étés réalisées avec
un programme écrit par Elisabeth Pichelin et l'auteur ; les
résultats en ont été visualisés grace au logiciel
Gnuplot de
Colin Kelley et Thomas Williams.
Document réalisé par Emmanuel Dormy