
Welcome
Introduction
Links and Refs
Standard Model
Accelerators
Relativity
Nobel Prizes
String Theory
Unification
Extra dimensions
Sociology
Duality
Internet
Branes
Black holes
M-Theory
Reactions
Black
 Black holes are called black,
because in the theory of general relativity, nothing can escape from a black
hole, not even light. Therefore a black hole will look like a black object
-- there's no light coming from a black hole. Nothing can escape from a
black hole, but we can go pretty close to it, and still have a chance to
escape. It is only when we are closer than a certain distance that we will
never be able to escape anymore. The critical distance to the black hole
is marked by the horizon. Indeed, anything behind the horizon will never
be seen again by an observer far from the black hole. Of course, he might
decide to travel past the horizon himself and might meet all kinds of aliens
that were hidden from his view before.
Black holes are called black,
because in the theory of general relativity, nothing can escape from a black
hole, not even light. Therefore a black hole will look like a black object
-- there's no light coming from a black hole. Nothing can escape from a
black hole, but we can go pretty close to it, and still have a chance to
escape. It is only when we are closer than a certain distance that we will
never be able to escape anymore. The critical distance to the black hole
is marked by the horizon. Indeed, anything behind the horizon will never
be seen again by an observer far from the black hole. Of course, he might
decide to travel past the horizon himself and might meet all kinds of aliens
that were hidden from his view before. 
Area
 The horizon of black holes turns
out to have very peculiar properties. When two black holes collide, because
they attract each other through the gravitational force, they will form
a new black hole, bigger than the one before. But the area of the horizon
of the new black hole will always be larger than the sum of the areas of
the two original black holes. That is a property very reminiscent of a main
property of entropy in the theory of the behavior of large systems under
temperature changes, volume changes, etc.
The horizon of black holes turns
out to have very peculiar properties. When two black holes collide, because
they attract each other through the gravitational force, they will form
a new black hole, bigger than the one before. But the area of the horizon
of the new black hole will always be larger than the sum of the areas of
the two original black holes. That is a property very reminiscent of a main
property of entropy in the theory of the behavior of large systems under
temperature changes, volume changes, etc.
Thermodynamics
The theory that tells us how gasses and solids behave when we heat them or cool them down is called thermodynamics. In thermodynamics, we characterize a system by its volume, its temperature, but also by its entropy. The entropy of a system tells us in how much disorder the system is in, and simultaneously, it tells us something about how many other states the system could easily change into. Indeed, when we have a pile of paper, by a small change in the pile of paper, most papers will still be in the same relative order. An ordered system has few other states it can easily change into. But when we have lots of papers spread all around our office floor, a breath of wind might rearrange the whole lot into another state of complete disorder, and we wouldn't know which. A state of disorder has many other states it can easily change into. The entropy, or disorder of a system therefore is a measure for the number of states that are easily available to a system.A crucial property of these many particle systems (like a glass of water with some ink particle in it) is that, when we leave them alone, they tend to go for the state of the most disorder (the ink particles flee all over the glass of water). Entropy increases in general.
Radiation
The analogy between the area of the horizon of the black hole increasing, and the entropy in thermodynamical systems increasing, turns out to be more than formal. Indeed, as Bekenstein taught us, we can associate an entropy to a black hole that is equal to the area of its horizon (up to a proportionality constant). When two black holes meet, or in any other process described by general relativity, the entropy of the total system will increase, since the total horizon area of the black hole formed in the process will increase. Thus, we are looking at our black hole as a thermodynamical system, with an associated entropy.Once we see our black hole as a thermodynamical system, and general relativity as the theory that describes the thermodynamics of black holes, we can ask other questions. What is the temperature of the black hole ? It turns out that indeed a black hole has a temperature associated with it, having to do with the strength of gravity at the horizon of the black hole. That poses a puzzle. We know that everything that has a certain temperature radiates heat. But general relativity tells us that black holes do not radiate at all.
Quantum corrections
A black hole radiates nothing in general relativity, but when looked at quantum-mechanically, it does. Stephen Hawking analyzed the quantum-mechanical process of particle pair production near the horizon of a black hole, and found that some particles were attracted into the black hole, while others managed to escape outward, such that the net effect was as if the black hole radiated. To an outside observer the black hole radiates particles, and precisely looks like an object with a temperature associated to the strength of the gravitational force at the horizon of the black hole.Statistical and Thermodynamical
We have identified our black hole with a thermodynamical system and general relativity as describing the thermodynamical properties of the black hole. That is very interesting, but it raises new questions. Indeed, in physics we are used to thermodynamical descriptions as being the large scale descriptions of systems that actually consist of a high number of particles or excitations. Usually, there is a so-called statistical mechanical description of these systems, that, when we average out all effects of the individual movements and properties of the different excitations, gives rise to the thermodynamical theory of the large system. A natural question to ask then is: what is the statistical mechanical description of black holes ?We already saw in Hawking's description of particle creation how a quantum mechanical theory serves as a microscopic explanation for a net large scale effect. Unfortunately, the theory that he used was highly dependent on the fact that he was describing an effect near the horizon of the black hole. If we want to have an overall statistical mechanical explanation of black holes, it is clear that we need an overall quantum mechanical theory of gravity. Luckily, this is exactly the topic we have been discussing in the previous chapters. String theory is a quantum mechanical description of gravity, so it should provide us with a statistical mechanical explanation of all thermodynamical properties of black holes. It includes the phenomenon of Hawking radiation. Is it successful in explaining the entropy Bekenstein associated to black holes ?
Supersymmetric
Actually, string theory includes black holes of many different types. One particular type are black holes that are very symmetric, indeed supersymmetric. The more symmetry the object under study has, the easier it is to study it, usually. That's why we start out by talking about supersymmetric black holes. 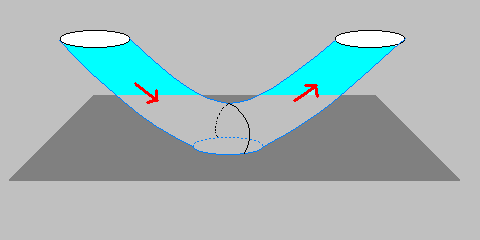 The supersymmetric
black holes indeed have an associated Bekenstein entropy, and Hawking
radiation. Does string theory give an explanation for the Bekenstein entropy
? It does give an explanation to a certain extent. Indeed, we can count
the number of microscopic states available to these supersymmetric black
holes, and this determines the entropy of the black hole. Unfortunately,
we are only able to do this in a regime where we expect stringy correction
to general
The supersymmetric
black holes indeed have an associated Bekenstein entropy, and Hawking
radiation. Does string theory give an explanation for the Bekenstein entropy
? It does give an explanation to a certain extent. Indeed, we can count
the number of microscopic states available to these supersymmetric black
holes, and this determines the entropy of the black hole. Unfortunately,
we are only able to do this in a regime where we expect stringy correction
to general 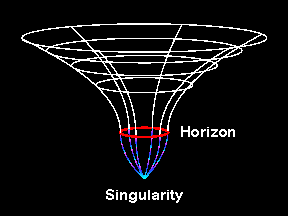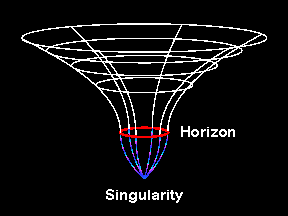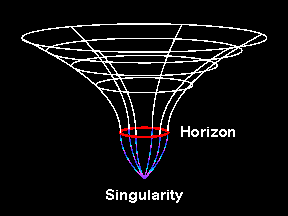 relativity
to become very important. Thus, our black hole wouldn't really be black
hole anymore, but some strange conglomerate of strings. Fortunately, however,
we got used to the fact that certain quantities, like the number of states
availably to a supersymmetric object, does not change as we change from
one regime into another. Thus, we expect the entropy we measure in another
regime still to be valid where general relativity is a good approximation.
And indeed, the entropy calculated from the statistical mechanical explanation
that string theory gives to general relativity agrees with the entropy
as predicted by Bekenstein. That is a major advance in our understanding
of the physics of black holes.
relativity
to become very important. Thus, our black hole wouldn't really be black
hole anymore, but some strange conglomerate of strings. Fortunately, however,
we got used to the fact that certain quantities, like the number of states
availably to a supersymmetric object, does not change as we change from
one regime into another. Thus, we expect the entropy we measure in another
regime still to be valid where general relativity is a good approximation.
And indeed, the entropy calculated from the statistical mechanical explanation
that string theory gives to general relativity agrees with the entropy
as predicted by Bekenstein. That is a major advance in our understanding
of the physics of black holes. 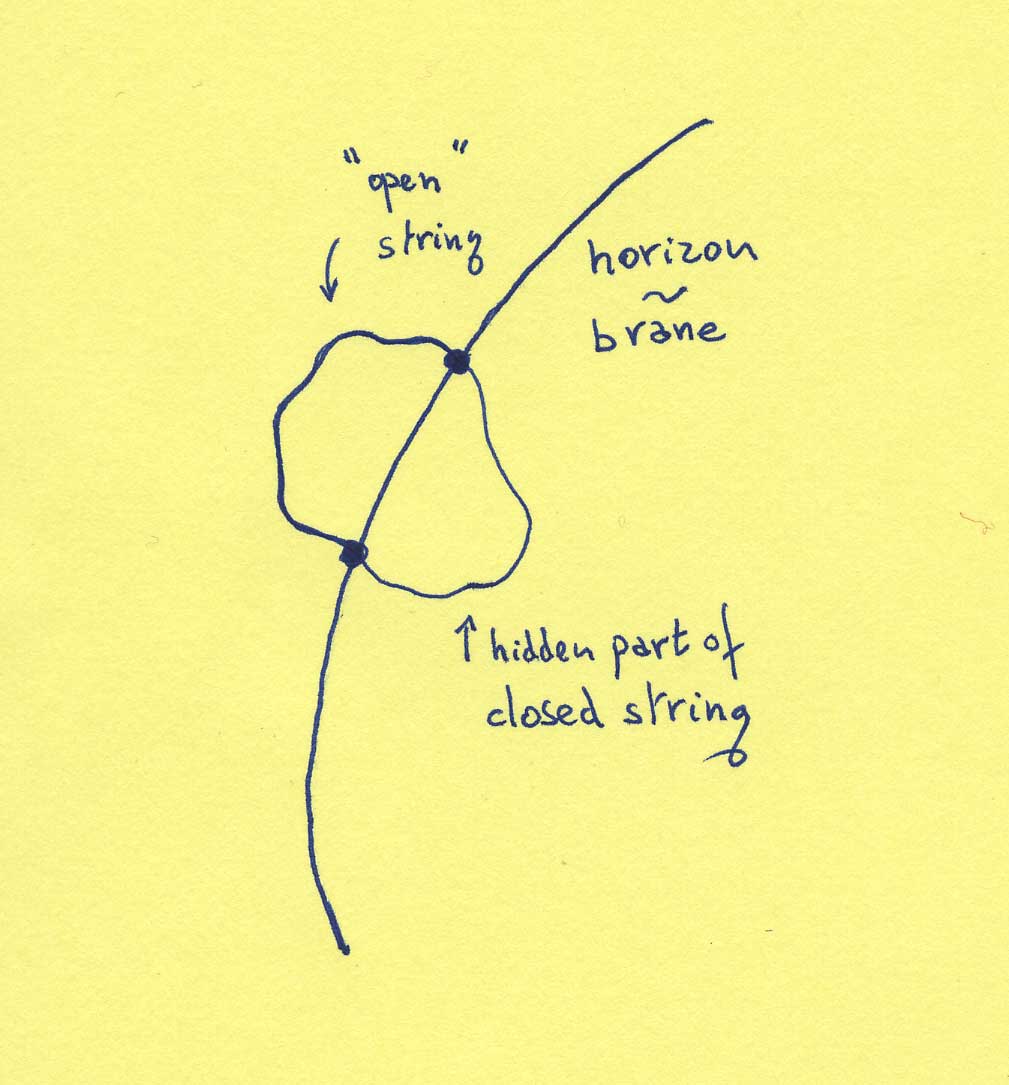
That does not mean that there are no puzzles left involving black holes.
Indeed, we still need to explain the entropy of non-supersymmetric black
holes and can only report minor progress in that area of research. Moreover,
certain paradoxes involving black holes still await a convincing resolution.
