Si la membrane était infiniment grande, on sent qu'assez loin de la baguette, elle serait parfaitement plate. En se rapprochant de la baguette, une pente apparaitraît, pente qui augmenterait au fur et à mesure qu'on s'en approche. Ce que nous donne l'analyse physique du problème, c'est la façon dont cette pente varie. C'est là l'équation de notre membrane. Il faut noter que la pente n'est elle même que la variation de la hauteur ; et finalement, tout le problème va être, connaissant ces variations, d'en déduire la hauteur en chaque point.
Ce problème - passer des variations d'une grandeur à la grandeur elle-même - est somme toute assez courant. Ainsi, on le rencontre en démographie ; lorsque l'on cherche , connaissant les taux de natalité et de mortalité à extrapoler la population dans cinquante ans. On le trouve encore lorsque, connaissant les variations instantanées d'un titre boursier, on veut en déduire son cours.
Pour la compréhension de ce qui va suivre, nous allons rappeler ici cette notion de dérivée. Le lecteur averti pourra sauter la lecture de cette section pour passer directement à la section 3.2.
Pour trouver la position de la membrane, nous allons avoir à résoudre des équations. Dans beaucoup de cas, ce qui nous intéresse (par exemple la forme de notre membrane) ne peut être représenté par un seul nombre, mais par une fonction (c'est-à-dire tout un ensemble de valeurs). Contrairement aux équations que l'on rencontre au lycée, dont les inconnues sont des nombres, les inconnues de nos équations seront donc des fonctions.
Imaginez que nous nous promenons sur un chemin à travers champs et collines, notre chemin va toujours tout droit, mais il monte et descend au gré des collines. Comment pourrait-on décrire l'allure de ce chemin ?
La première idée qui vienne à l'esprit est de donner à chaque endroit l'altitude à laquelle on se trouve, c'est la notion de fonction. Quelqu'un disposant de cette information peut parfaitement se représenter notre chemin, il peut même le dessiner ( cf figure 4).
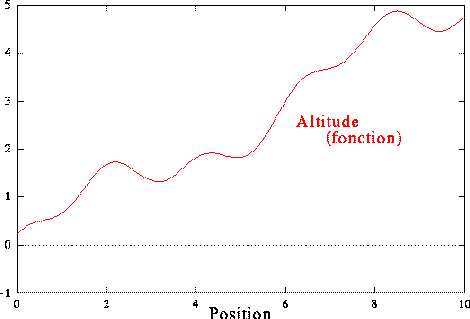
Figure 4 : La connaissance de l'altitude en chaque point permet de définir
de façon unique la forme de ce chemin.
Peut-on, comme pour la démographie ou la bourse, définir le chemin par ses variations ? Supposons que nous connaissions en chaque endroit la pente du chemin (c'est-à-dire la façon dont le chemin monte ou descend). Cela ne suffirait-il pas ?
Pour pouvoir utiliser cette notion de variation, il faut d'abord nous mettre d'accord sur une convention pour mesurer la pente. Le plus courant dans la vie de tous les jours est de mesurer une pente en pour cent (0 % pour l'horizontale, 100% pour la verticale) ou en degrés d'angles (0 degrés pour l'horizontale, 90 pour la verticale). Une troisième convention est adoptée par les mathématiciens, elle peut se définir par : <<De combien de pas dois-je monter pour pouvoir avancer d'un pas vers l'avant ?>> (ce qui revient à prendre la tangente trigonométrique de l'angle). La pente ainsi définie est nulle pour l'horizontale et infinie pour la verticale. La pente est positive lorsque le chemin monte, négative quand il descend.
Essayons à présent de reconstruire la fonction à partir de l'ensemble de ses pentes. Partons d'un point, et avançons en suivant ces informations. Nous pouvons bien dessiner le chemin. Cette idée est explicitée sur la figure 5. Remarquons enfin que la connaissance de l'ensemble des pentes constitue elle aussi une fonction ; on l'appelle la dérivée.
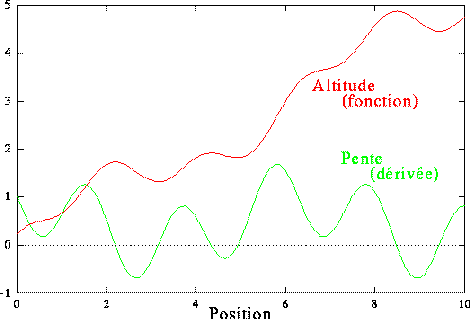
Figure 5 : La connaissance de la pente en chaque point permet également de
définir de façon unique la forme du chemin (pour peu que l'on ait un
point de départ).
Voici donc un cas simple, nous savons à présent ce qu'est la dérivée d'une fonction (l'ensemble des pentes en chaque point).
Continuons donc d'avancer sur notre chemin... Voici que tout à coup, on ne sait pourquoi, le chemin vient à disparaître, nous pouvons alors continuer tout droit ou bien changer de direction, en fait nous sommes libres ! Fort bien, mais nous voulons à présent définir le lieu où nous nous trouvons...
Nous pouvons comme tout à l'heure définir en chaque point l'altitude, mais qu'en est-il de notre dérivée, autrement dit de la pente en chaque point. Horreur et stupéfaction ! La pente dépend de la direction. Plaçons nous en un point de la colline : si nous tournons sur nous-même, la pente varie avec la direction dans laquelle on regarde... Heureusement : par deux droites de l'espace sécantes en un seul point, il ne passe qu'un seul plan ! Si nous mesurons la pente dans deux directions distinctes, nous définissons en fait deux droites, donc un plan unique, qui nous permet de connaître la pente dans toutes les directions. Nous en concluons que si nous choisissons deux directions (perpendiculaires par exemple), et que nous donnons en chaque point la pente dans chacune de ces deux directions, nous aurons parfaitement défini notre colline... Par exemple, si l'on connait en un point la pente vers le Nord et celle vers l'Est, on peut en déduire en les combinant la pente dans n'importe quelle direction.
Le point important est donc que, pour caractériser cette infinité de pentes, il suffit de donner la pente selon deux directions distinctes.
Nous avons alors comme pour le chemin deux façons de définir l'endroit où nous sommes, soit de donner en chaque point notre altitude, soit de donner en chaque point les pentes dans les deux directions choisies. Pour le chemin (espace à une dimension) l'ensemble des pentes était unique et s'appellait dérivée, pour la colline (espace à deux dimensions) on parle pour chacune des deux directions de dérivée partielle (puisque chacune prise indépendamment ne fournit qu'une information partielle sur la pente).
Il faut cependant ajouter que ces notions peuvent se compliquer à loisir : par exemple, de la même façon que l'on est passé du chemin à la colline, on peut continuer à augmenter la dimension de l'espace, indéfiniment...(le lecteur intéressé par cette notion la trouvera développée dans le livre de Ian Stewart Dieu joue-t-il aux dés ? Chapitre 5). Ou encore, puisque la dérivée est elle-même une fonction, pourquoi ne pas la définir non pas par ses valeurs, mais par ses propres variations, ses pentes ? C'est ce que l'on appelle la dérivée seconde (et cette opération peut elle-même être répétée indéfiniment, sous certaines conditions de régularité).
Document réalisé par Emmanuel Dormy