``Solving the strongly coupled 2D gravity: 2. Fractional spin operators and topological three point functions'', Nucl. Phys. B426 (1994) 140.
La motivation de ce travail, en collaboration avec J.-F. Roussel, a été de complèter
mon étude précédente du couplage fort (voir page ![]() ) qui ne
discutait que le cas de spins demi-entiers (en utilisant les opérateurs
chiraux du type
) qui ne
discutait que le cas de spins demi-entiers (en utilisant les opérateurs
chiraux du type
![]() seuls bien connus
à l'époque). Ceci est insuffisant pour terminer la discussion car les poids conformes de
l'espace
seuls bien connus
à l'époque). Ceci est insuffisant pour terminer la discussion car les poids conformes de
l'espace
![]() , où le théorème de découplage unitaire est vérifié,
correspondent à des spins rationnels mais pas forcément entiers. Si l'on veut
préserver la symétrie entre opérateurs et états de l'espace d'Hilbert, il faut
donc traiter le cas d'opérateurs avec spins rationnels, ce qui est aussi compliqué que
celui des spins continus. Ceci fait, nous avons pu généraliser le théorème de
troncation de façon à rétablir complètement la symétrie entre spectre de
vecteurs de plus haut poids des modules de Verma et spectre de poids conformes des opérateurs
primaires.
, où le théorème de découplage unitaire est vérifié,
correspondent à des spins rationnels mais pas forcément entiers. Si l'on veut
préserver la symétrie entre opérateurs et états de l'espace d'Hilbert, il faut
donc traiter le cas d'opérateurs avec spins rationnels, ce qui est aussi compliqué que
celui des spins continus. Ceci fait, nous avons pu généraliser le théorème de
troncation de façon à rétablir complètement la symétrie entre spectre de
vecteurs de plus haut poids des modules de Verma et spectre de poids conformes des opérateurs
primaires.
Notre méthode a été d'étendre le bootstrap chiral (solutions des équations polynomiales de Moore et Seiberg) obtenu précédemment en collaboration avec E. Cremmer, au cas des représentations semi-infinies à spin continu avec nombres d'écran entiers non négatifs; ce qui détermine complètement les matrices de fusion et échange. En particulier nous avons vérifié que nos 6j généralisés satisfont bien les identités du type Racah et Bidenharn-Elliot. Nous avons démontré le découplage de deux familles d'opérateurs physiques chiraux, aux valeurs spéciales de la charges centrales, en obtenant une solution complète des équations de Moore Seiberg sous-jacentes. La généralisation peut se concevoir le mieux en termes du nombre d'identités triangulaires imposées aux vertex, qui est de trois dans le cas habituel (appelé cas 3PI) et que nous avons pu réduire de façon cohérente soit à deux (2PI) soit à un (1PI).
Pour les valeurs spéciales qui
peuvent se mettre sous la forme,
![]() , il y a deux espaces
physiques possibles qui sont donnés par
, il y a deux espaces
physiques possibles qui sont donnés par
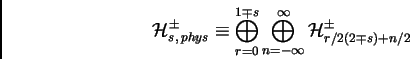
![\fbox{\begin{minipage}[t]{13cm} {\sl Th\'eor\\lq emes de troncation:
\par
Pour $C=1...
...{\cal H}_{ s,\, phys}^{+}$(resp. ${\cal H}_{s,\, phys}^{-}$).
} \end{minipage}}](img150.png)