- ... supersym\'etrie1
- au moins dans les pays de l'Ouest
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
consid\'er\'e2
- originellement introduit par
Schwinger et Gell-Mann, Lévy
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cr\'eation)3
- le cas
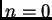 décrit la position du centre de gravité de la corde
décrit la position du centre de gravité de la corde
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dimensions4
- Cette
dernière idée a été
aussi mise en avant par M. Virasoro
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
l'\'epoque5
- déjà exprimée dans le travail de
Hsue,
Sakita et Virasoro
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... type6
- dans cet exemple on
suppose tous les
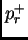 positifs
positifs
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... conditions7
- également proposées par Kaku et Kikkawa,
et considérées par Goldstone dans un travail non publié
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... applications8
- que je n'ai pas
suivies en détail
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... jauge9
- Elle a été récemment
étendue à Yang-Mills supersymétrique
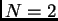 par
W. Siegel.
par
W. Siegel.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bords10
- dans le cas sans bord Liouville
lui-même a résolu cette question au niveau classique
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ncide11
- en fait il y a, dans notre méthode,
une double représentation
en général
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... unité''
12
- mise en
évidence dans l'approche de Curtright, Thorn et collaborateurs
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Olive13
- Contrairement au cas habituel, il existe deux projections
de G-parités différentes qui conduisent à l'égalité des
fonctions de partition.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ouvertes14
- Ceci est maintenant
résolu dans une large part, come on le verra plus loin.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... corde15
- La situation n'est
pas cependant complètement claire du point de vue de
la résolution de super-Liouville, comme nous le verrons plus loin
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... th\'eories16
-
voirsection 1.3.2 pour quelques explications générales
sur leur structure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Zamolodchikov
17
- incluant un opérateur de spin 3 en plus des
générateurs de Virasoro.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
simple18
- associée à
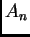 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... principe19
- sauf pour les modèles de type
topologique comme nous le verrons plus loin.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...R\'ef\'erences20
- le prétirage a été publié en deux articles
séparés
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... quantique
21
- contrairement à ce qui
avait été supposé le facteur de proportionalité ne peut être
éliminé.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... usuelles22
- Pour éviter
d'entrer dans le détail de la théorie des représentations, nous nous sommes limités
aux théories irrationnelles.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... traverser23
- bien sûr, cette
barrière se déplace si la symétrie bidimensionnelle change de
nature.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... r\'esulte24
- pour les opérateurs du type
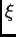 , les seuls que je pouvais utiliser
à l'époque. Voir plus loin pour les opérateurs
, les seuls que je pouvais utiliser
à l'époque. Voir plus loin pour les opérateurs 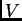 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
consid\'er\'e25
- L'espace
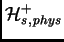 coïncide avec l'espace
coïncide avec l'espace
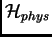 mentionné au paragraphe C1.4.
mentionné au paragraphe C1.4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... d'ann\'ees26
- Dans l'article hep-th/9911008
à paraître dans le volume de commémoration de Y. Golfand, j'ai écrit un prologue relatant
l'histoire de ma contribution personnelle à cette découverte, en collaboration avec B. Sakita.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.