



Next: Groupes quantiques associés aux
Up:
Previous: Gravité quantique en couplage
Contents
Les théories de Toda
Ces théories sont extrêmement intéressantes
à plus d'un titre. Pour introduire ce qui va suivre il est utile de revenir sur
leur principe de base élégamment formulé par Lesnov et Saveliev
et qui est très simple. Soient 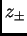 des coordonnées complexes
(
des coordonnées complexes
(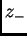 est le complexe conjugué de
est le complexe conjugué de 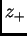 ),
), 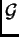 une algèbre de Lie simple
et
une algèbre de Lie simple
et
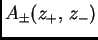 un champ de jauge à valeur dans
un champ de jauge à valeur dans 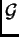 . La paire
de Lax
est obtenue en imposant tout d'abord qu'il soit une pure jauge:
. La paire
de Lax
est obtenue en imposant tout d'abord qu'il soit une pure jauge:
![\begin{displaymath}
\partial_{z_-}A_+-\partial_{z_+}A_-+ \Bigl [A_+,\, A_-\Bigr ]=0.
\end{displaymath}](img163.png)
Choisissons (il en existe toujours) une graduation de 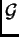 , c'est à
dire une décomposition
de la forme
, c'est à
dire une décomposition
de la forme
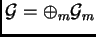 où
où 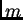 prend des valeurs entières et telle que
le commutateur d'un élément de
prend des valeurs entières et telle que
le commutateur d'un élément de 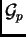 avec un élément de
avec un élément de 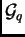 soit
dans
soit
dans
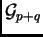 . Les équations de Toda considérées habituellement
sont caractérisées par le fait que l'on choisit de plus
. Les équations de Toda considérées habituellement
sont caractérisées par le fait que l'on choisit de plus
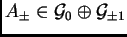 . Elles sont donc déterminées par le
choix de
. Elles sont donc déterminées par le
choix de 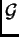 et par le choix de la graduation. Lorsque cette graduation est celle qui
est appelée principale on l'appelle la théorie de Toda associée à
et par le choix de la graduation. Lorsque cette graduation est celle qui
est appelée principale on l'appelle la théorie de Toda associée à 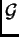 . C'est de
ce type dont nous avons parlé jusqu'à présent et que nous considérerons de nouveau
plus loin aux paragraphes 1.4.1-1.4.4. Un autre
choix de graduation, avec la même condition sur
. C'est de
ce type dont nous avons parlé jusqu'à présent et que nous considérerons de nouveau
plus loin aux paragraphes 1.4.1-1.4.4. Un autre
choix de graduation, avec la même condition sur 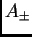 est considéré au
paragraphe 1.4.5. Clairement la composante
est considéré au
paragraphe 1.4.5. Clairement la composante
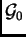 est une sous-algèbre de
est une sous-algèbre de 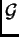 . Comme le choix de 1.4.5
donne un
. Comme le choix de 1.4.5
donne un 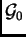 non abélien, ces théories sont distinguées par le
même qualificatif. Finalement pour un choix de graduation donné ont peut
prendre
non abélien, ces théories sont distinguées par le
même qualificatif. Finalement pour un choix de graduation donné ont peut
prendre
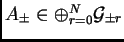 ,
,
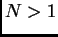 . Ce cas appelé ``généralisation de plus haute graduation'' est le sujet des
deux derniers paragraphes.
. Ce cas appelé ``généralisation de plus haute graduation'' est le sujet des
deux derniers paragraphes.
Rappelons, de plus, qu'il
existe deux grandes catégories de théories de Toda
: soit 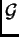 est une algèbre de Lie simple de
dimension finie, auquel cas la théorie est invariante conforme, soit
est une algèbre de Lie simple de
dimension finie, auquel cas la théorie est invariante conforme, soit
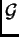 est une algèbre de Lie affine. Dans ce dernier cas on a une théorie de particules
relativistes massives. Dans ce rapport, il s'agit toujours du premier cas, sauf dans le dernier
paragraphe.
est une algèbre de Lie affine. Dans ce dernier cas on a une théorie de particules
relativistes massives. Dans ce rapport, il s'agit toujours du premier cas, sauf dans le dernier
paragraphe.
Subsections




Next: Groupes quantiques associés aux
Up:
Previous: Gravité quantique en couplage
Contents
Jean-Loup Gervais
2001-10-25
![]() est une algèbre de Lie simple de
dimension finie, auquel cas la théorie est invariante conforme, soit
est une algèbre de Lie simple de
dimension finie, auquel cas la théorie est invariante conforme, soit
![]() est une algèbre de Lie affine. Dans ce dernier cas on a une théorie de particules
relativistes massives. Dans ce rapport, il s'agit toujours du premier cas, sauf dans le dernier
paragraphe.
est une algèbre de Lie affine. Dans ce dernier cas on a une théorie de particules
relativistes massives. Dans ce rapport, il s'agit toujours du premier cas, sauf dans le dernier
paragraphe.